「Rによるやさしい統計学」で学ぶR言語と統計学の基礎徹底解説2-5章

R言語と統計学を同時に学ぶことができる『Rによるやさしい統計学』を少しずつ読み進めています。

この本は難しい数学の式などは出てこずに、わかりやすい言葉や例で統計学の基礎的なキーワードとそれに紐づく「Rの使い方」に焦点を当て、説明をしてくれています。個人的には事前に基本的な概念を説明した入門書を一冊やってから、「Rではどうやるか？」を知るにオススメな本だと思います。

まだ前半戦の状態ですが、この中で特に覚えておきたい部分を中心にメモを書いていきます。

🐠 2章： 1つの変数の記述統計

データ解析の出発点となる『1つの変数』の記述方法についての説明。

😀 レクチャー

# c: データの値を結合させる
a <- c(1, 2, 5, 10, 15, 5)< span>

# ベクトル/行列の要素の平均 (行平均, 列平均)
mean(a) #=> 6.333333

# 中央値
median(a) #=> 5

# 頻度を整理して得られる分布である「度数分布」の表を作る
table(a)
a
 1  2  5 10 15 
 1  1  2  1  1 

# 不偏分散
## 確率変数の分布が期待値からどれだけ散らばっているかを示す値。
var(a)

# 標準偏差
## ある集団についてのデータがどのように分布しているかを表す値。
sd(a)
sqrt(mean((a-mean(a))^2))

## 標本分散の関数を自作
varp <- function(x) {< span>
    標本分散 <- var(x)*(length(x) - 1) length(x)< span>
    標本分散
}
varp(a)

## 別ファイルの関数の読み込み
source("varp.R")

例題やってみた

a <- c(60,100,50,40,50,230,120,240,200,30)< span>
b <- c(50,60,40,50,100,80,30,20,100,120)< span>

# 1)
hist(a)

Rplot03

hist(b)

Rplot

# 2)
mean(a)
sqrt(mean((a-mean(a))^2)) # 標準偏差
mean(b)
sqrt(mean((b-mean(b))^2)) # 標準偏差

# 3)
(a - mean(a))/sqrt(mean((a-mean(a))^2))
(b - mean(b))/sqrt(mean((b-mean(b))^2))

🐰 3章： 2つの変数の記述統計

『2つの変数における量的変数における関係、質的変数における関係』についての説明です。ちなみに量的変数と質的変数の説明は次のとおり。

😸 レクチャー

* 量的変数: データ間に優劣や大小が比較できる。『テストの点数』のような数値データ
=> 比率データ: 絶対的なゼロ点を有する(質量、長さ、年齢、時間、金額など)
=> 間隔データ: 数値(メモリ)の間隔が等しい(気温、知能指数など)

* 質的変数： データ間に優劣がなく、大小関係が比較できない。「男・女」や「好き・嫌い」など
=> 順序データ： 大小関係(順序)のみ意味をもつ(満足度、選好度、硬度など)
=> 名義データ： 内容を区別するために便宜的に割りあている(電話番号、性別など)

さらに、相関(correlation)と回帰(regression)の説明は次のとおり。

相関 correlation #=> xとyの間に区別をもうけず対等に見る見方や方法
回帰 regression  #=> ｘからyを見る(yからxを見る)方法

# 分散図(グラフの表示)
a <- c(1,2,3,4,5)< span>
b <- a * 2< span>
plot(a, b)

Rplot01

# 共分散(数値)
## 2つのデータが、どれだけ関連性・連動性があるかを示す係数
cov(a, b) #=> 5
#=> sum((a-mean(a))*(b-mean(b)))/length(a) と同義
#=> mean((a-mean(a))*(b-mean(b))) と同義

# 相関係数
## 2つのデータが、どれだけ関連性があるのかを示す係数
cor(a, b) #=> 1
#=> cov(a, b)/(sd(a)*sd(b))と同義

相関係数は-1 <= r <="1で次のように関係性がわかります。

-0.2 <= r <="0.2" #> ほとんど相関なし
-0.4 <= r < -0.2, 0.2 #> 弱い相関あり
-0.7 <= r < 0.4, 0.4 #> 中程度の相関あり
-1.0 <= r < -0.7, 0.7 #> 強い相関あり

# クロス集計表
## 質的変数の関係について表す
math <- c('like', 'hate', 'like', 'hate')< span>
statistics <- c('hate', 'like', 'hate', 'like')< span>
table(math, statistics)
      statistics
math   hate like
  hate    0    2
  like    2    1

# ファイ係数
## 1と0の２つの値からなる変数（二値変数）に対して計算される相関係数
## math(数学)、statistics(統計)の好き=>1、嫌い=>0に変換して考える
math_zero <- ifelse(math="='like'," 1, 0)< span>
math_zero #=> 1 0 1 1 0
statistics_zero <- ifelse(statistics="='like'," 1, 0)< span>
statistics_zero #=> 0 1 0 1 1
cor(math_zero, statistics_zero)

例題やってみた

# 1) 散布図
hour <- c(1,3,10,12,6,3,8,4,1,5)< span>
score <- c(20,40,100,80,50,50,70,50,10,60)< span>
plot(hour, score)

Rplot02

# 2) 相関係数
cor(hour, score)
#=>  0.9092974 なので高い相関がある

# 3) クロス統計
youwa <- c('洋食', '和食', '洋食', '和食')< span>
amakara <- c('甘党', '辛党', '甘党', '辛党')< span>
table(youwa, amakara)
# amakara
# youwa  甘党 辛党
# 洋食    6    4
# 和食    3    7

# 4) ファイ係数
youwa_zo <- ifelse(youwa="='洋食'," 1, 0)< span>
amaka_zo <- ifelse(amakara="='甘党'," 1, 0)< span>
cor(youwa_zo, amaka_zo)
#=> 0.3015113

Rの便利メソッド

# Rのメソッド
# ifelse(条件, 真の場合, 偽の場合) 場合分けをする
hour <- c(1,3,10,12,6,3,8,4,1,5)< span>
hour_zo <- ifelse(hour>= 5, "up", "down")
#=> "down" "down" "up"   "up"   "up"   "down" "up"   "down" "down" "up"

🎂 第4章：母集団と標本

大きな集団(母集団)から取り出した少数のデータ(標本)を使って『もとの集団の性質について推測する』ための推測統計の基本的な理論についての学習。

母集団と標本の説明はこちら。

母集団: データ全体を指す。国民全体、工業製品全体など
標本: 母集団から取り出したデータの一部

推測統計の分類についてはこちら。

推定: 具体的な数値を用いて『母数の値は◯◯くらいだろう』という結論を導くこと
点推定: 1つの値で空いての結果を表す。日本の中学生の数学平均点が「60点」と推定
区間推定: ある程度の幅を持った区間で結果を表す。数学平均が『50-70点』と推定

## サイコロを6回ふった場合、サイコロのすべての目が1回ずつ出るのは稀
dice6 <- ceiling(runif(n="6," min="0," max="6))
table(dice6)
# dice6
# 2 3 4 
# 1 2 3

## サイコロを600万回ふった場合、1/6に限りなく近づく
dice6m <- ceiling(runif(n="6000000," min="0," max="6))
table(dice6m)
# dice6m
# 1       2       3       4       5       6 
# 999612 1000211  998870  999613 1000366 1001328 

table(dice6m)/6000000
# dice6m
# 1         2         3         4         5         6 
# 0.1666020 0.1667018 0.1664783 0.1666022 0.1667277 0.1668880

# 男性が2/3、女性が1/3を表す棒グラフ
barplot(c(2/3, 1/3), names.arg=c('man', 'woman'))

スクリーンショット 2014-02-16 8.12.38

# 正規分布
## ある1つの数値を目標とした作業で偶然生じる偶然的な誤差の分布
curve(dnorm(x, mean=0, sd=1), from=-4, to=4)

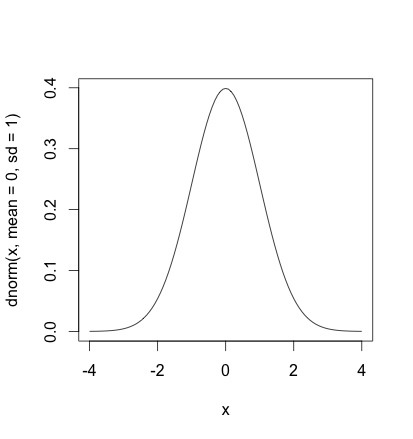
Rplot01

# 母集団が正規分布であるような集団から無作為標本を抽出
## ランダムに5つの標本を取得
hyohon <- rnorm(n="5," mean="50," sd="10)
#=> 62.69624 40.50412 51.14337 58.89571 36.13923

## ヒストグラムを作成
hist(hyohon)

Rplot03

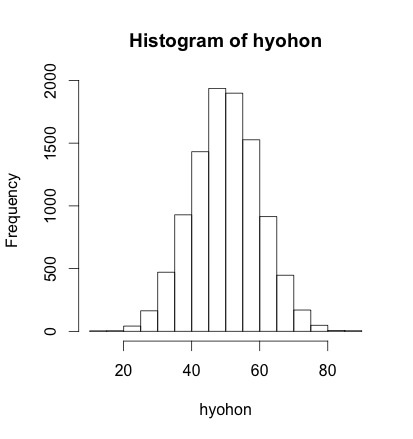
上のように標本数が少ないと、正規分布かどうかはわかりません。ただし、サンプルサイズをある程度大きくするとヒストグラムは正規分布に近いものになっていきます。

# 標本数を増やした場合のヒストグラム => 正規分布に近づく
hyohon <- rnorm(n="10000," mean="50," sd="10)" #> 正規分布に近いヒストグラムになる
hist(hyohon)

Rplot04

練習問題をやってみた

# 1) 経験的な標本分布
ave <- numeric(length="5000)
for(i in 1:5000) {
  hyohon <- rnorm(n="20," mean="50," sd="10)
  ave[i] <- mean(hyohon)< span>
}
hist(ave, freq=FALSE)
curve(dnorm(x, mean=50, sd=sqrt(100/20)), add=TRUE)

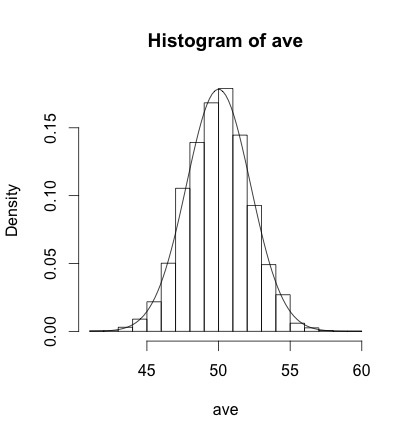
Rplot05

# 2) 理論的な標本分布
curve(dnorm(x, sd=sqrt(1/25)), -3, 3)
curve(dnorm(x, sd=sqrt(1/16)), -3, 3, add=TRUE)
curve(dnorm(x, sd=sqrt(1/9)),  -3, 3, add=TRUE)
curve(dnorm(x, sd=sqrt(1/4)),  -3, 3, add=TRUE)
curve(dnorm(x, sd=sqrt(1/1)),  -3, 3, add=TRUE)

Rplot06

本章で出てくるRの関数

# 小数点以下の切り上げ
ceiling(1.5) #=> 2

# 一様分布に従う乱数を発生させる
runif(n=4, min=6, max=12) 
[1]  8.430616 11.064664  9.835286 10.971259

# 決まったパターンの乱数を発生させる
set.seed(1) #=> 乱数の種を1に設定するこれを指定後は常に同じ乱数が発生する

# 棒グラフを作成
barplot(c(2/3, 1/3), names.arg=c("man", "woman"))

# 関数の曲線を描く
curve(dnorm(x), from=-3, to=3)

# 正規分布の確率密度変数
dnorm(0, mean=0, sd=1)

# 正規分布に従う乱数を発生
rnorm(n=5, mean=50, sd=10)

# 数値を格納する領域の確保
a <- numeric(length="10000)

# 連続データを作る
## 0から20までの整数の連続データをつくる
1:20
[1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

# 正規分布の確率密度関数
dnorm(0, mean=0, sd=1) #=> 0.3989423

# 棒グラフを作成
barplot(c(3/4, 1/4), names.arg=c('man', 'woman'))

# 関数の曲線を描く => curve()
## 正規分布のグラフが出力する場合
curve(dnorm(x), from=-3, to=3)

🎉 第5章：統計的仮説検定

検定の手順

1) 母集団に関する帰無仮説と対立仮説を設定する
2) 検定統計量を選ぶ
3) 有意水準αの値を決める
4) データから検定統計量の実現値を求める
5) 検定統計量の実現値が棄却域に入る => 対立仮説を採用する

検定のキーワード

帰無仮説　　　#=>「差がない」、「効果が無い」という仮説
対立仮説　　　#=> 帰無仮説に反して「差がある」という仮説
検定統計量　　#=> 検定に用いられる標本統計量のこと
有意水準　　　#=> 帰無仮説を棄却し対立仮説を採択する基準
棄却域     　#=> 非常に生じにくい検定統計量の値の範囲 
ｐ値　　　　　#=> 帰無仮説が正しい仮説で、標本から計算した検定統計量を実現できる確率
第１種の誤り　#=> 「帰無仮説が真の時にこれを棄却する」誤り
第２種の誤り　#=> 「帰無仮説が偽の時にこれを採択する」誤り
検定力　　　　#=> 間違っている仮説を正しく棄却できる確率のこと(100% - 第２種の誤りの確率)

標準正規分布を用いた検定の例題をやってみた

# 標準正規分布を用いた検定の検定統計量 :
Z = mean(x) - 標準正規分布の平均/sqrt(標準正規分布の分散/標本数)

sinri <- c(13, 14, 7, 12, 10, 6, 8, 15, 4, 9, 5, 15)< span>
Z <- (mean(sinri) - 12) sqrt(10 length(sinri))< span>
qnorm(0.025, lower.tail=FALSE)
qnorm(0.025) #=> -1.959964
qnorm(0.975) #=> 1.959964
Z < qnorm(0.025) #=> TRUEなので帰無仮説を棄却

# pnorm関数からp値を求める
2*pnorm(abs(Z), lower.tail=FALSE) 
#=> 0.004677735 < 有意水準0.05となるので帰無仮説を棄却

t分布を用いた検定の例題をやってみた

先述の「標準正規分布を用いた検定」は母集団の分散が計算に必須です。そこで、未知の母集団の分散の代わりに、自由度(データの標本数 - 1)のt分布を元に計算する検定があります。

# t分布を用いた検定の検定統計量 :
t = (mean(x) - 母集団の平均)/sqrt(t分布の分散/標本数)

# 5.4 例題
# 帰無仮説「心理テスト(sinri)の平均は12である」のt検定
sinri <- c(13, 14, 7, 12, 10, 6, 8, 15, 4, 9, 5, 15)< span>
t <- (mean(sinri) -12) sqrt(var(sinri) length(sinri)) #> 2.616648

# qt(p, df)で自由度dfの場合の下側確率pとなるt値が求まる
qt(0.025, 19) #=> -2.093024
qt(0.975, 19) #=> 2.093024

t < qt(0.025, 19)  
#=> TRUEなので帰無仮説を棄却

# 関数t.testによる検定
t.test(sinri, mu=12)
# One Sample t-test
# data:  sinri
# t = -2.6166, df = 19, p-value = 0.01697
# alternative hypothesis: true mean is not equal to 12
# 95 percent confidence interval:
#   8.400225 11.599775
# sample estimates:
#   mean of x 
# 10

無相関検定の例題をやってみた

母集団において相関が0であることを検定するための手法。

# t分布を用いた検定の検定統計量 :
t = (標本相関 * sqrt(標本数 - 2))/sqrt(1 - 標本相関)

## 帰無仮説 => toukei1とtoukei2の相関係数は0である
toukei1 <- c(6,10,6,10,5,3,5,9,3,3,11,6,11,9,7,5,8,7,7,9)< span>
toukei2 <- c(10,13,8,15,8,6,9,10,7,3,18,14,18,11,12,5,7,12,7,7)< span>
t <- (cor(toukei1, toukei2)*sqrt(20-2)) sqrt(1-cor(toukei1,toukei2)^2)< span>

qt(0.025, 18) #=> -2.100922
qt(0.975, 18) #=>  2.100922
qt(0.975, 18) < t #=> TRUEとなるので帰無仮説は棄却 => 相関はある

# 無相関検定を実行する関数cor.text
cor.test(toukei1, toukei2)
# Pearson's product-moment correlation
# 
# data:  toukei1 and toukei2
# t = 4.8057, df = 18, p-value = 0.0001416
# alternative hypothesis: true correlation is not equal to 0
# 95 percent confidence interval:
#  0.4596086 0.8952048
# sample estimates:
#      cor 
# 0.749659

独立性の検定(χ2乗検定)の例題をやってみた

## 帰無仮説 => 「数学の好き嫌い」と「統計の好き嫌い」には差がない
math <- c("hate", "hate", "like", "hate")< span>
staitstics <- c("like", "like", "hate", "hate")< span>
table(math, staitstics)
# staitstics
# math   hate like
# hate   10    4
# like    2    4

exp_hate_hate = 12 * 14/20
exp_like_hate = 12 *  6/20
exp_hate_like =  8 * 14/20
exp_like_like =  8 *  6/20
exp_dosu <- c(exp_hate_hate, exp_like_hate, exp_hate_like, exp_like_like)< span>
#=> 8.4 3.6 5.6 2.4

kansoku_dosu <- c(10,2,4,4)< span>
kai_nizyo <- sum((exp_dosu -kansoku_dosu)^2 exp_dosu)< span>
#=> 2.539683

# χ 2乗分布に従う棄却域を求める => qchisq関数
qchisq(0.95, 1) < kai_nizyo #=> FALSE
## 結論: 「数学の好き嫌い」と「統計の好き嫌い」には優位な差はない

## χ2乗検定を行う関数 correct=FALSEは連続性の補正を行わないオプション
chisq.test(table(math, staitstics), correct=FALSE)
# Pearson's Chi-squared test
# 
# data:  table(math, staitstics)
# X-squared = 2.5397, df = 1, p-value = 0.111
#=> pが0.11で0.05よりも大きな値なので帰無仮説が採択される

練習問題をやってみた

## 1)
# 帰無仮説 : 平均170cmの正規分布に従うサンプルである
height <- c(165, 150, 170, 168, 159, 167, 178, 155, 161, 162, 166, 171, 160, 172, 167)< span>
t.test(height, mu=170) 
# One Sample t-test
# 
# data:  height
# t = -3.8503, df = 19, p-value = 0.001079
# alternative hypothesis: true mean is not equal to 170
# 95 percent confidence interval:
#   160.584 167.216
# sample estimates:
#   mean of x 
# 163.9 
#=> p = 0.00107で 0.05より小さいので帰無仮説は棄却

## 2)
## 帰無仮説 : 勉強時間とテスト結果には相関性がない
hour <- c(1,3,10,12,6,3,8,4,1,5)< span>
score <- c(20,40,100,80,50,50,70,50,10,60)< span>
cor.test(hour, score)
# Pearson's product-moment correlation
# 
# data:  hour and score
# t = 6.1802, df = 8, p-value = 0.0002651
# alternative hypothesis: true correlation is not equal to 0
# 95 percent confidence interval:
#  0.6542283 0.9786369
# sample estimates:
#       cor 
# 0.9092974 

## 3)
## スピアマンの順位相関係数
## http://goo.gl/sFitJ

cor.test(hour, score, method="spearman")
# Spearman's rank correlation rho
# 
# data:  hour and score
# S = 10.1822, p-value = 5.887e-05
# alternative hypothesis: true rho is not equal to 0
# sample estimates:
#       rho 
# 0.9382895 

## ケンドールの順位相関係数
## http://goo.gl/2HRaa

cor.test(hour, score, method="kendall")
# Kendall's rank correlation tau
# 
# data:  hour and score
# z = 3.2937, p-value = 0.0009889
# alternative hypothesis: true tau is not equal to 0
# sample estimates:
# tau 
# 0.8471174 

## 4) χ2乗検定
youwa <- c('洋食', '和食', '洋食', '和食')< span>
amakara <- c('甘党', '辛党', '甘党', '辛党')< span>
chisq.test(youwa, amakara)
# Pearson's Chi-squared test with Yates' continuity correction
# 
# data:  youwa and amakara
# X-squared = 0.8081, df = 1, p-value = 0.3687

## 5-1) 無相関検定
lang <- c(60, 40, 30, 70, 55)< span>
soci <- c(80, 25, 35, 70, 50)< span>
cor.test(lang, soci)
# Pearson's product-moment correlation
# 
# data:  lang and soci
# t = 2.6952, df = 3, p-value = 0.07408
# alternative hypothesis: true correlation is not equal to 0
# 95 percent confidence interval:
# -0.1590624  0.9892731
# sample estimates:
# cor 
# 0.841263 
#=> p値が有意水準(0.05)より高いので2つの結果に相関はない

## 5-2) 無相関検定 : 同じサンプルを2回使う
lang2 <- rep(lang, 2)< span>
soci2 <- rep(soci, 2)< span>
cor.test(lang2, soci2)
# Pearson's product-moment correlation
# 
# data:  lang2 and soci2
# t = 4.4013, df = 8, p-value = 0.002283
# alternative hypothesis: true correlation is not equal to 0
# 95 percent confidence interval:
#  0.4499858 0.9615658
# sample estimates:
#      cor 
# 0.841263 
#=> p値が有意水準(0.05)より低いので2つの結果に相関はある

#=> (5-1)と(5-2)は相関係数(cor)は一致するがp値が大きく異る

便利なRの関数

# 標準正規分布の下側確率に対応する値
qnorm(0.025) #=> -1.959964

# 標準正規分布の下側確率
pnorm(-1.959964) #=> 0.025

# t分布で下側確率に対応する値
qt(0.025, 19) #=> -2.093024

# t分布の下側確率
pt(-2.093024, 19) #=> 0.025

# カイ二乗分布の下側確率に対応する値
qchisq(0.95, 1) #=> 3.841459

# カイ二乗分布の下側確率に対応する値
pchisq(3.841459, 1) #=> 0.95

# t分布の確率
dt(1, 19) #=> 0.2357406

# カイ二乗分布の確率密度分布
dchisq(3.841,1) #=> 0.02982808

🖥 VULTRおすすめ

「VULTR」はVPSサーバのサービスです。日本にリージョンがあり、最安は512MBで2.5ドル/月($0.004/時間)で借りることができます。4GBメモリでも月20ドルです。最近はVULTRのヘビーユーザーになので、「ここ」から会員登録してもらえるとサービス開発が捗ります！

酒と泪とRubyとRailsと

「Rによるやさしい統計学」で学ぶR言語と統計学の基礎徹底解説2-5章

🐠 2章： 1つの変数の記述統計

😀 レクチャー

例題やってみた

🐰 3章： 2つの変数の記述統計

😸 レクチャー

例題やってみた

Rの便利メソッド

🎂 第4章：母集団と標本

練習問題をやってみた

本章で出てくるRの関数

🎉 第5章：統計的仮説検定

検定の手順

検定のキーワード

標準正規分布を用いた検定の例題をやってみた

t分布を用いた検定の例題をやってみた

無相関検定の例題をやってみた

独立性の検定(χ2乗検定)の例題をやってみた

練習問題をやってみた

便利なRの関数

🖥 VULTRおすすめ

📚 おすすめの書籍

🐠 2章： 1つの変数の記述統計

😀 レクチャー

例題やってみた

🐰 3章： 2つの変数の記述統計

😸 レクチャー

例題やってみた

Rの便利メソッド

🎂 第4章： 母集団と標本

練習問題をやってみた

本章で出てくるRの関数

🎉 第5章： 統計的仮説検定

検定の手順

検定のキーワード

標準正規分布を用いた検定の例題をやってみた

t分布を用いた検定の例題をやってみた

無相関検定の例題をやってみた

独立性の検定(χ2乗検定)の例題をやってみた

練習問題をやってみた

便利なRの関数

🖥 VULTRおすすめ

📚 おすすめの書籍

🎂 第4章：母集団と標本

🎉 第5章：統計的仮説検定