「R Tips」で学ぶR言語のプログラミング的Tips


統計学やR言語を勉強していく過程で、R言語のプログラミング的な側面や言語仕様をちゃんと理解したいと思うようになりました。ということでチャンレンジしたのが、『R-Tips』です。

このサイトはいくつかのトピックに分かれているので、自分のRの使い方に合わせて勉強しや少なっています。まだまだ前半戦ですが、特に覚えておきたいコマンドを中心にメモを書いていきます。

(03/22 10:50) 回帰分析部分の説明を追記


Rの便利なメソッド

x <- "1245"< span>

# 中身についての情報を取得
str(x) #=> chr "1245"
summary(x)
# Length     Class      Mode 
# 1 character character

# 基本的な情報
y <- c(2, 3, 4, 5)< span>
summary(y)
# Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
# 2.00    2.75    3.50    3.50    4.25    5.00

ベクトルの生成

# aからbまでのベクトルを生成 => a:b
1:10 
#=> 1  2  3  4  5  6  7  8  9 10

# (a, b)間をn等分するベクトルを生成 => seq(a, b, length = n)
seq(1, 2, length = 10)
# 1.000000 1.111111 1.222222 1.333333 1.444444
# 1.555556 1.666667 1.777778 1.888889 2.000000

# aからbまでcずつ増加するベクトルを生成 => seq(a, b, by = c)
seq(2, 15, by=3) 
#=> 2  5  8 11 14

# a:bをc回繰り返すベクトルを生成 => rep(a:b, times = c)
rep(1:3, times = 2)
#=> 1 2 3 1 2 3

# ベクトル内の値をユニークにする(重複した値を取り除く) => unique(x)
unique(c(1,2,4,6,3,3,2,1))
#=> 1 2 4 6 3

# 0をn個並べたベクトルを生成 
numeric(5)
#=> 0 0 0 0 0

x <- 1:5< span>
# 要素の並びを逆順にする
rev(x)
#=> 5 4 3 2 1

y <- 5:1< span>
# 要素の並び順を整列させる
sort(y)
#=> 1 2 3 4 5

ベクトル条件

# どれか一つでも条件をみたすものがあるか？
any(y > 4) #=> TRUE

# すべて条件をみたすか？
all(y > 2) #=> FALSE

# NULLか否か
is.null(NULL) #=> TRUE

# NA(データの欠損)か否か
is.na(NA) #=> TRUE

# NaN(数では表せない)か否か
is.nan(0/0) #=> TRUE

# 有限か否か
is.finite(1) #=> TRUE

# 無限か否か
is.infinite(1/0) #=> TRUE

ベクトルの中身

x <- 1:5< span>
# 2-4番目の要素
x[2:4] #=> 2, 3, 4

# 1, 4番目の要素以外を取り出す
x[c(-1,-4)] #=> 2, 3, 5

# 3より大きい要素を取り出す
x[3 < x] #=> 4, 5

# 1より大きく、4より小さい要素を取り出す
x[1 < x & x < 4] #=> 2, 3

y <- x * 2< span>
# 条件を満たす要素の番号を返す
(1:length(y))[1 < y & y < 8]
#=> 1, 2, 3

日付

# 日付型に変換
as.Date("2012/08/15")
#=> "2012-08-15"
as.Date("20130222", format="%Y%m%d")
#=> "2013-02-22"

# 現在時刻を日付オブジェクトで取得
today <- sys.date()< span>
now <- sys.time()< span>

# 日付の差分
x <- as.date(c("2012 07 01", "2009 08 01"))< span>
x[2] - x[1]
#=> Time difference of -1065 days

文字列

# 文字列ベクトルの結合
paste(month.abb, 1:8, c("st", "nd", "rd", rep("th",5)))
# "Jan 1 st" "Feb 2 nd" "Mar 3 rd" "Apr 4 th" "May 5 th" "Jun 6 th" 
# "Jul 7 th" "Aug 8 th" "Sep 1 st" "Oct 2 nd" "Nov 3 rd" "Dec 4 th"

# 文字列から特定の部分を切り出し
substring("defghijklmnopqr", 3, 7) 
#=> "fghij"

データフレーム

# データフレームの作成
sex <- c(rep("f", 3), rep("m", 1))< span>
height <- seq(150, 180, length="4)
weight <- seq(70, 80, length="4)
df <- data.frame(sex, height, weight)< span>
# sex height   weight
# 1   F    150 70.00000
# 2   F    160 73.33333
# 3   F    170 76.66667
# 4   M    180 80.00000

# データオブジェクトの行数を返す
nrow(df) #=> 4

# summaryでデータフレームの要素の情報を表示
summary(df)
# sex       height          weight    
# F:3   Min.   :150.0   Min.   :70.0  
# M:1   1st Qu.:157.5   1st Qu.:72.5  
# Median :165.0   Median :75.0  
# Mean   :165.0   Mean   :75.0  
# 3rd Qu.:172.5   3rd Qu.:77.5  
# Max.   :180.0   Max.   :80.0 

# heightで降順に並べ直し
sort_list <- order(df$height,decreasing="T)
df[sort_list,]
# sex height   weight
# 4   M    180 80.00000
# 3   F    170 76.66667
# 2   F    160 73.33333
# 1   F    150 70.00000

# typeカラムに条件に応じてBIG, MIDDLE, SMALL
df$type <- ifelse(height>= 170, "BIG", ifelse(height>=160, "MIDDLE", "SMALL"))
# sex height   weight   type
# 1   F    150 70.00000  SMALL
# 2   F    160 73.33333 MIDDLE
# 3   F    170 76.66667    BIG
# 4   M    180 80.00000    BIG

# 一律でheight_mmカラムを追加
transform(df, height_mm=df$height*100)
# sex height   weight   type height_mm
# 1   F    150 70.00000  SMALL     15000
# 2   F    160 73.33333 MIDDLE     16000
# 3   F    170 76.66667    BIG     17000
# 4   M    180 80.00000    BIG     18000

# 行番号を追加
df$id <- row.names(df)< span>
# sex height   weight   type id
# 1   F    150 70.00000  SMALL  1
# 2   F    160 73.33333 MIDDLE  2
# 3   F    170 76.66667    BIG  3
# 4   M    180 80.00000    BIG  4

# 行方向の結合
cbind(df, df)
# sex height   weight   type id sex height   weight   type id
# 1   F    150 70.00000  SMALL  1   F    150 70.00000  SMALL  1
# 2   F    160 73.33333 MIDDLE  2   F    160 73.33333 MIDDLE  2
# 3   F    170 76.66667    BIG  3   F    170 76.66667    BIG  3
# 4   M    180 80.00000    BIG  4   M    180 80.00000    BIG  4

# 列方向の結合
rbind(df, df)
# sex height   weight   type id
# 1   F    150 70.00000  SMALL  1
# 2   F    160 73.33333 MIDDLE  2
# 3   F    170 76.66667    BIG  3
# 4   M    180 80.00000    BIG  4
# 5   F    150 70.00000  SMALL  1
# 6   F    160 73.33333 MIDDLE  2
# 7   F    170 76.66667    BIG  3
# 8   M    180 80.00000    BIG  4

🐠 サンプルデータセット

Rで勉強していく上で、避けて通れないのがサンプルデータの確保です。Rにはデフォルトで複数のデータセットが格納されています。『統計を学びたい人へ贈る、統計解析に使えるデータセットまとめ』に初心者にお勧めなデータがまとめられています！

🚜 データセットを使った集計・グラフ表示

デフォルトのデータセットのあやめのデータ(iris)を使って、いくつかサンプルを書いていきます。

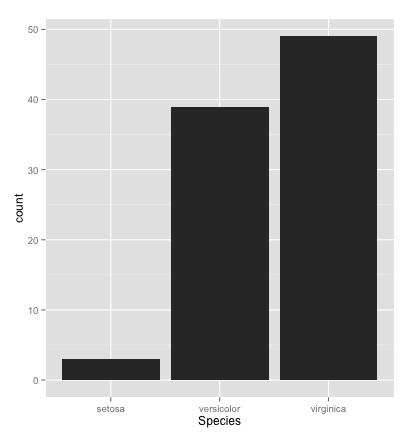
# irisはあやめのデータ・セット
width_set <- iris[,c("sepal.length", "petal.length", "species")]< span>
width_large <- width_set[width_set$species="=" "versicolor",]< span>
mean(width_large$Petal.Length) #=> 4.26

# plyrパッケージの導入
# plyr : データフレームの加工をしやすくするパッケージ
install.packages("plyr")
library("plyr")

# irisのデータからSpeciesをキーにSepal.Length(がくの長さ)の平均を出す
data <- ddply(iris, .(species), summarise, sepal.length.average="mean(Sepal.Length))
# Species Sepal.Length.Average
# 1     setosa                5.006
# 2 versicolor                5.936
# 3  virginica                6.588

# Sepal.Length(がくの長さ)の平均順でならべ直す
arrange(data, desc(Sepal.Length.Average))
# Species Sepal.Length.Average
# 1  virginica                6.588
# 2 versicolor                5.936
# 3     setosa                5.006

# 棒グラフ
# 棒グラフは「月ごとの販売実績」のように書くカテゴリの度数や比率を表示するために利用する
index <- iris$sepal.length> 5.5
dat <- iris[index,]< span>
xtabs(~Species, data=dat, drop.unused.levels=T)
# Species
# setosa versicolor  virginica 
# 3         39         49
qplot(Species, data=dat, geom="bar")

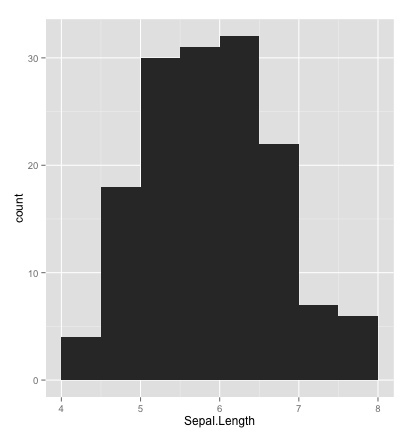
Rplot01

# ヒストグラム
# 身長・成績・人口などのように連続量のデータの度数(割合)を表示する
qplot(Sepal.Length, data=iris, geom="histogram", binwidth=0.5, xlim=c(4,8))

Rplot

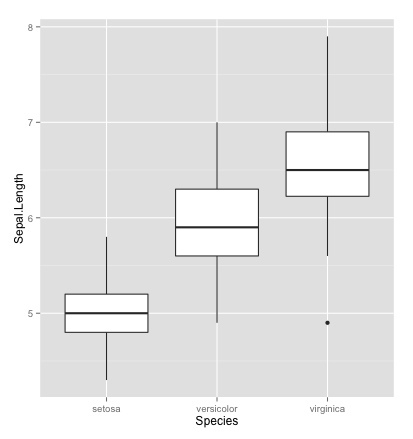
# 箱ひげ図
# カテゴリごとの中央値、箱、ヒゲ、外れ値を表示。ヒストグラムの簡略版
# 1つが複数カテゴリのデータ、もう一つが連続量の場合に用いる
qplot(Species, Sepal.Length, data=iris, geom="boxplot")

Rplot02

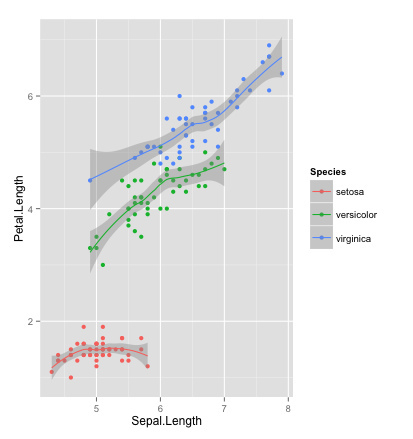
# 散布図
# 2つの変数の値に従って座標平面上に複数の点を表示
# 2つの変数がともに連続量の場合に用いる
index <- iris$species !="virginica" < span>
dat <- iris[index,]< span>
qplot(Sepal.Length, Petal.Length, data=iris, geom=c("point", "smooth"), color=Species)

Rplot03

🐮 サンプルデータを使った単回帰分析

サンプルデータを知らなすぎて、あまり適切な分析ではないですが、手元にある範囲内で。

キーワード

独立変数: 原因となる変数
従属変数: 性質を明らかにしたい側の変数
単回帰分析: 独立変数が1つの分析
重回帰分析: 独立変数が2つ以上の分析

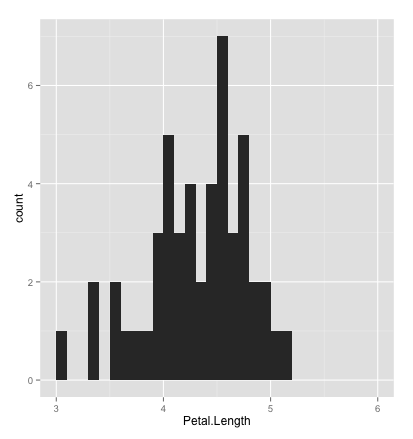
# データ・セットを使った回帰分析のサンプル
library(ggplot2)
qplot(Petal.Length, data=dat, geom="histogram", bandwith=0.5, xlim=c(3,6))

index <- iris$species="=" 'versicolor'< span>
dat <- iris[index,]< span>
result <- glm(sepal.length~petal.length, data="dat," family="gaussian)
summary(result)
# glm(formula = Sepal.Length ~ Petal.Length, family = gaussian, 
#     data = dat)
# 
# Deviance Residuals: 
#   Min        1Q    Median        3Q       Max  
# -0.73479  -0.20272  -0.02065   0.26092   0.69956  
# 
# Coefficients:
#   Estimate Std. Error t value Pr(>|t|)    
# (Intercept)    2.4075     0.4463   5.395 2.08e-06 ***
#   Petal.Length   0.8283     0.1041   7.954 2.59e-10 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# (Dispersion parameter for gaussian family taken to be 0.1173364)
# 
# Null deviance: 13.0552  on 49  degrees of freedom
# Residual deviance:  5.6321  on 48  degrees of freedom
# AIC: 38.717
# 
# Number of Fisher Scoring iterations: 2
#=> 回帰式 y = ax + bで a = 2.4075, b = 0.8283
#=> Coefficientsの最後が信頼度。'***'なので高い

🤔 適切な回帰分析式の比較

AIC : 赤池情報量規準

統計モデルの良さを評価するための指標。

統計モデルの比較

こちらも素人のトライですので、ツッコミお待ちしています！

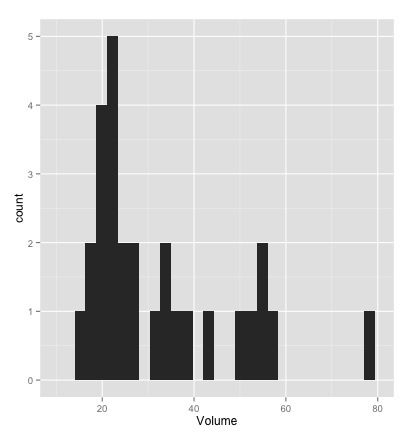
library(ggplot2)
# 単純にヒストグラムでプロット
qplot(Volume, data=trees, geom="histogram", bandwith=5, xlim=c(10,80))

Rplot

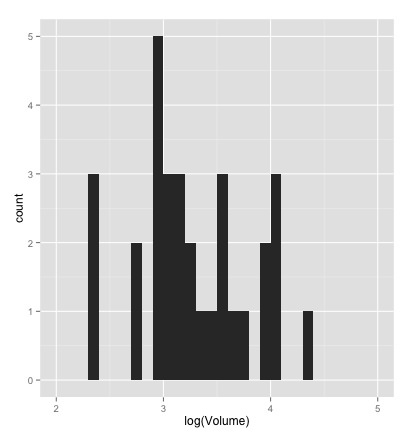
# 対数をとってヒストグラムでプロット
qplot(log(Volume), data=trees, geom="histogram", bandwith=0.2, xlim=c(2,5))

Rplot02

本来は正規分布に従いそうなデータですが、サンプルデータを目視する限りは対数正規分布に近そう。

result <- glm(volume~girth, data="trees," family="gaussian)
summary(result)  
# (Intercept) -36.9435     3.3651  -10.98 7.62e-12 ***
#   Girth         5.0659     0.2474   20.48  < 2e-16 ***
# AIC: 181.64

result <- glm(volume~girth, data="trees," family="gaussian(link="log"))
summary(result)
# (Intercept) 1.340516   0.097224   13.79 2.89e-14 ***
#   Girth       0.147910   0.005839   25.33  < 2e-16 ***
# AIC: 169.14

result <- glm(volume~(girth+height), data="trees," family="gaussian)
summary(result)
# (Intercept) -57.9877     8.6382  -6.713 2.75e-07 ***
#   Girth         4.7082     0.2643  17.816  < 2e-16 ***
#   Height        0.3393     0.1302   2.607   0.0145 *  
# AIC: 176.91

result <- glm(volume~(girth+height), data="trees," family="gaussian(link="log"))
summary(result)
# (Intercept) 0.679294   0.258124   2.632  0.01366 *  
#   Girth       0.134163   0.006845  19.601  < 2e-16 ***
#   Height      0.011144   0.003975   2.804  0.00907 ** 
# AIC: 163.37

#=> 上記4つのAIC(赤池情報量規準)からみると一番最後の回帰式(対数正規分布で独立変数にGirth, Heightをとる)が最も近い

🐞 ポワソン回帰

ポワソン回帰は離散値かつ、ゼロ以上の範囲のデータを扱うときに利用する。

適切なデータでないんで、雰囲気だけメモ。

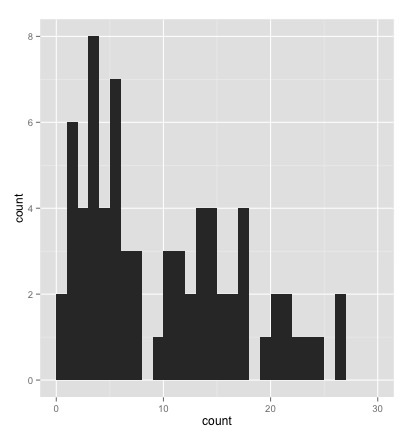
dat <- insectsprays < span>
qplot(count, data=dat, geom="histogram", bandwith=1, xlim=c(0,30))

Rplot04

result <- glm(count~spray, data="dat," family="poisson(link="log"))
summary(result)
# (Intercept)  2.67415    0.07581  35.274  < 2e-16 ***
#   sprayB       0.05588    0.10574   0.528    0.597    
#   sprayC      -1.94018    0.21389  -9.071  < 2e-16 ***
#   sprayD      -1.08152    0.15065  -7.179 7.03e-13 ***
#   sprayE      -1.42139    0.17192  -8.268  < 2e-16 ***
#   sprayF       0.13926    0.10367   1.343    0.179   
# AIC: 376.59

🗽 独立変数の最適化

複数の独立変数から、Rが効率的なアルゴリズムで自動的にモデル選択をする方法。

適切なサンプルデータで後でリトライする予定…

# 独立変数の最適化
dat <- iris< span>
result <- glm(petal.width~sepal.length+sepal.width+petal.length, data="dat," family="gaussian(link="log"))
step(result, direction="backward")
# Start:  AIC=19.47
# Petal.Width ~ Sepal.Length + Sepal.Width + Petal.Length
# 
# Df Deviance     AIC
# - Sepal.Width   1    9.472  19.337
#                9.355  19.469
# - Sepal.Length  1   12.225  57.615
# - Petal.Length  1   33.293 207.890
# 
# Step:  AIC=19.34
# Petal.Width ~ Sepal.Length + Petal.Length
# 
# Df Deviance     AIC
#                9.472  19.337
# - Sepal.Length  1   12.371  57.394
# - Petal.Length  1   38.191 226.476
# 
# Call:  glm(formula = Petal.Width ~ Sepal.Length + Petal.Length, family = gaussian(link = "log"), 
#            data = dat)
# 
# Coefficients:
#   (Intercept)  Sepal.Length  Petal.Length  
# -0.3528       -0.2442        0.4752  
# 
# Degrees of Freedom: 149 Total (i.e. Null);  147 Residual
# Null Deviance:      86.57 
# Residual Deviance: 9.472  AIC: 19.34
#
#=> 以上より、Petal.Width = -0.2442*Sepal.Length + 0.4752*Petal.Length + -0.3528 がAICでベスト

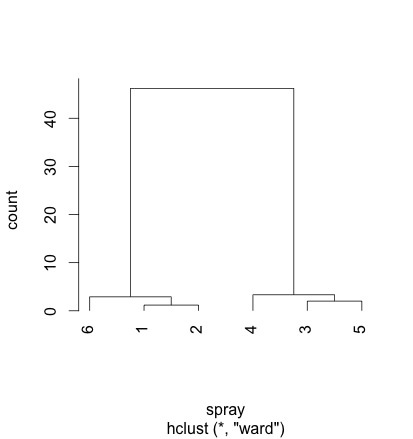
🏈 ユークリッド距離を使ったクラスタリング

ユークリッド距離や重心の概念を使ってクラスタリングを行う。

Rに難儀しているので、とりあえず暫定でできたところまで。使い方を覚えたらちゃんと直したい！

library("plyr")
dat <- insectsprays< span>
dat2 <- ddply(dat, .(spray), summarise, count_ave="mean(count))
distw <- dist(dat2, method="euclidean" )< span>
clust <- hclust(distw, method="ward" )< span>
plclust(clust, hang=-1, xlab="spray", ylab="count")

Rplot03

🍄 参考リンク

「plyrパッケージで君も前処理スタ☆」改め「plyrパッケージ徹底入門」

第30回R勉強会＠東京(#TokyoR)の資料

🎃 あとで読む

統計・機械学習・データマイニングの無料で読めるPDF資料


オンラインで無料公開されている書籍等のPDF資料をまとめ。

統計的機械学習 | 中川研究室


統計的機械学習とは、観測されたデータから統計的手法を用い新たな知識を導出すること。 統計的機械学習には種々の分類がある、この説明。

一般向けのDeep Learning


PFI 全体セミナーで発表した、専門家向けではなく一般向けのDeep Learning（深層学習）の解説です。どのような場面で活躍しているのか、今までの学習手法と何が違うのかを解説しています。

統計検定：Japan Statistical Society Certificate


「統計検定」とは、統計に関する知識や活用力を評価する全国統一試験です。 データに基づいて客観的に判断し、科学的に問題を解決する能力は、仕事や研究をするための21世紀型スキルとして国際社会で広く認められています。

チュートリアル | グローバル消費インテリジェンス寄附講座


GCI チュートリアル (Global Consumer Intelligence Tutorial) は、東京大学工学部 松尾豊研究室とグローバル消費インテリジェンス寄附講座の学生のためのチュートリアルです。ウェブと人工知能を活かした研究を行うために必要な技能を身に付けることを目的としています。

🚌 変更来歴

(03/15 10:45) 回帰に関する記述を追記

(03/21 17:25) データ・フレームを追記

(03/22 10:50) 回帰分析部分の説明を追記

🖥 VULTRおすすめ

「VULTR」はVPSサーバのサービスです。日本にリージョンがあり、最安は512MBで2.5ドル/月($0.004/時間)で借りることができます。4GBメモリでも月20ドルです。 最近はVULTRのヘビーユーザーになので、「ここ」から会員登録してもらえるとサービス開発が捗ります！

📚 おすすめの書籍