『アルゴリズムのキホン』を読みました & AOJでやってみた！ 【書評】

数年前に読んだ『アルゴリズムのキホン』を再勉強も兼ねて読みなおしています。プログラミングの基礎力を高めるのが今の目標なので徹底的に頑張ります！

ちなみに、アルゴリズム系を勉強するときにオススメなのが、会津大学が提供している『Aizu Online Judge』です。
日本語の問題も多数ありますし、何よりほかの人の回答があるので、効率的なコードを参考にできるのがよいです。
また、新しい言語を勉強するときにも、パズルをとくような感覚で勉強していけるのですごくいい練習になると思います！

データ構造

🐝 ハッシュテーブル

データを入力値としたハッシュ関数により得られる値が、ルート配列の要素番号となる

データ構造

1) ルート配列と呼ばれる要素数Nの配列
2) ルート配列の要素を先頭ポインタとするリスト => ルート配列の各要素がデータを管理

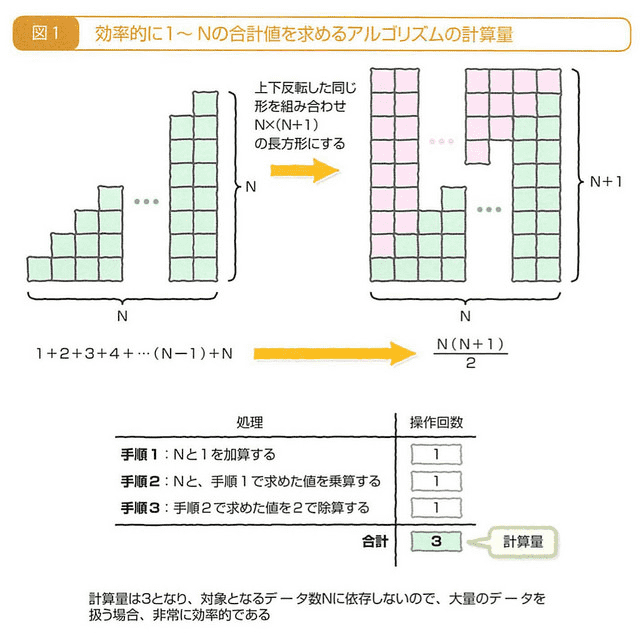
アルゴリズム

🤔 計算量

• アルゴリズムの効率性は、「時間計算量」と「領域計算量」に着目する
• 時間計算量 =「演算」「条件比較」などの処理の操作回数で表す
• 領域計算量 = 使用するメモリ領域の大きさを表す

• O(1) => Nに依存しない計算量
• O(n) => 計算量がNに比例する
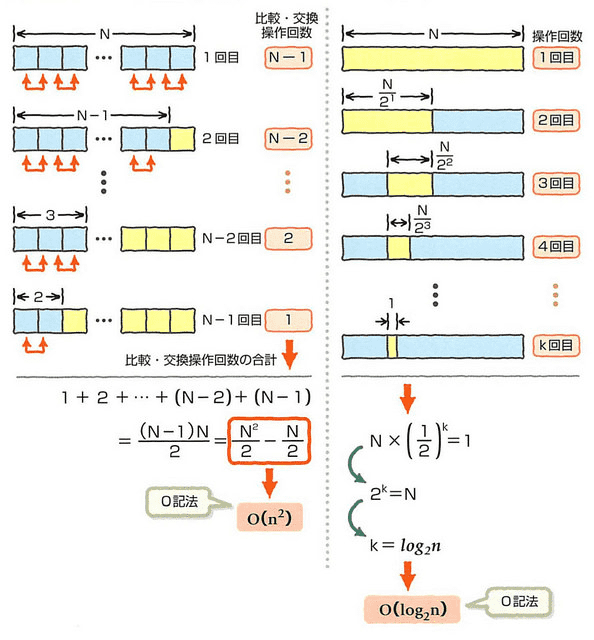
• O(n**2) => NxN会の操作がひつような計算。バブルソートなど
• O(log2n) => 二分木探索(バイナリサーチ)のような1回操作するたびに1/2に狭まる計算量

🗻 ソートアルゴリズムの種類

選択ソート

• データの中から最小値(最大値)を見つけ出して、先頭(末尾)のデータと交換を行う

バブルソート

• 隣り合うデータどうしを比較して、大小関係が正しくなるように並び替える

マージソート

• ソート対象データ列を分割していき、再度マージすることで並び替える

クイックソート

• データ列から任意の数を選び、その値との大小で2分割することを繰り返して並び替える

🐮 ユークリッドの互除法

概要

ユークリッドの互除法 - Wikipedia

Rubyで最小公倍数を求める

サンプル問題(AOJ)

GCD and LCM - Aizu Online Judge

Aizu Online Judgeの最大公約数(GCM: the greatest common divisor)と、最小公倍数(LCM: least common multiple)を求める問題。

Rubyのサンプルソース

class Array
  # 最大公約数: ２つ以上の正の整数に共通な約数（公約数）のうち最大のもの
  def lcm
    self.inject do |a, b|
      a*b/self.gcd
    end
  end

  # 最小公倍数: ２つ以上の正の整数の共通な倍数（公倍数）のうち最小のもの
  # ユークリッドの互除法
  def gcd
    self.inject do |a, b|
      while b > 0
        a, b = b, a if a < b
        a, b = b, a%b
      end
      return a
    end
  end
end

while str = gets
  a = str.split(' ').map(&:to_i)
  puts "#{a.gcd} #{a.lcm}"
end

# output
# 2 24
# 10000000 150000000

Pythonのサンプルソース

# coding:utf-8
import sys

# 最大公約数
def gcd(a, b):
  while b > 0:
    a, b = b, a%b
  return a

# 最小公倍数
def lcm(a, b):
  return a*b/gcd(a, b)

for s in sys.stdin:
  a, b = map(int,s.split())
  gcd_num = gcd(a, b)
  lcm_num = lcm(a, b)
  print "%d %d"%(gcd_num, lcm_num)

# output
# 2 24
# 10000000 150000000

🐹 動的計画法

概要

動的計画法を簡単に説明すると、「途中経過をメモしておいて、次の計算で使う」こと。

• 最強最速アルゴリズマー養成講座：アルゴリズマーの登竜門、「動的計画法・メモ化再帰」はこんなに簡単だった (2/5) - ITmedia エンタープライズ

サンプル問題(AOJ)

A First Grader

Aizu Online Judge。動的計画法を使って数式のパターン数を計算する問題。

Rubyサンプルソース

n = gets.to_i
arr = gets.split(' ').map(&:to_i)
dp = Array.new(n-1) { Array.new(21, 0) }
answer = arr[n-1]
dp[0][arr[0]] = 1

1.upto(n-2) do |i|
  0.upto(20) do |j|
    next if dp[i-1][j] == 0
    add = j + arr[i]
    sub = j - arr[i]

    dp[i][add] += dp[i-1][j] if add <= 20    dp[i][sub] += dp[i-1][j] if sub >= 0  endendputs dp[n-2][answer]
    dp[i][sub] += dp[i-1][j] if sub >= 0
  end
end

puts dp[n-2][answer]

Pythonサンプルソース

n = input()
arr = map(int, raw_input().split())
answer = arr[n-1]

dp = [[0]*21 for i in range(n)]
dp[0][arr[0]] = 1

for i in range(1, n-1):
  for j in range(21):
    if dp[i-1][j] == 0: continue
    vp = j + arr[i]
    vm = j - arr[i]

    if vp <= 20:      dp[i][vp] += dp[i-1][j]    if vm >= 0:      dp[i][vm] += dp[i-1][j]print dp[n-2][answer]
      dp[i][vp] += dp[i-1][j]
    if vm >= 0:
      dp[i][vm] += dp[i-1][j]

print dp[n-2][answer]

🎉 ポーカーの手札から役を求める

サンプル問題

Poker Hand

ポーカーの手札から役を答える問題。そんなに難しくない問題なので頭の体操にピッタリ！

Rubyのサンプルソース

while s = gets do
  cards = s.split(',').map(&:to_i)
  card_count = Array.new(13){0}
  cards.each { |c| card_count[c-1] += 1 }
  str = card_count.join
  card_count.delete(0)

  scr = 'null'
  case card_count.sort
    when [1,4]
      scr = 'four card'
    when [2,3]
      scr = 'full house'
    when [1,1,1,1,1]
      scr = 'straight' if str =~ /1{5}/ or str =~ /10{8}1{4}/
    when [1,1,3]
      scr = 'three card'
    when [1,2,2]
      scr = 'two pair'
    when [1,1,1,2]
      scr = 'one pair'
  end
  puts scr
end

Pythonのサンプルソース

import sys
for s in sys.stdin:
  hand = sorted(map(int, s.split(',')))
  kind = len(set(hand))
  ma = max([hand.count(i) for i in hand])

  ans = 'null'
  if kind == 4:
    ans = 'one pair'
  elif kind == 3:
    if ma == 2:
      ans = 'two pair'
    else:
      ans = 'three card'
  elif kind == 2:
    if ma==4:
      ans = 'four card'
    else:
      ans = 'full house'
  else:
    if hand == [1,10,11,12,13] or (hand[4] - hand[0]) == 4:
      ans = 'straight'
  print ans

🏈 Aizu Online Judgeのサンプルソース

当面はAOJを解きながら、アルゴリズムの再勉強をしていくつもりです。Ruby/PythonでのAOJの回答は下のリポジトリに保存しておきます。もしツッコミとかあればぜひ＾＾

morizyun/aoj-ruby-python - GitHub

🐡 変更来歴

• (2014-04-29 14:55) 動的計画法の解法を追加
• (2014-05-01 20:50) ポーカーの手札の解法を追加
• (2017-03-12 08:40) 各種調整

🐠 Secial Thanks

• 動的計画法が苦手な人が、動的計画法が超苦手な人へアドバイスしてみる

🖥 VULTRおすすめ

「VULTR」はVPSサーバのサービスです。日本にリージョンがあり、最安は512MBで2.5ドル/月($0.004/時間)で借りることができます。4GBメモリでも月20ドルです。 最近はVULTRのヘビーユーザーになので、「ここ」から会員登録してもらえるとサービス開発が捗ります！

📚 おすすめの書籍