統計解析の勉強をしていく中で、どうやったら実際の業務の中に活かしていけるかを模索していて、この本にいきあたりました。人々が生み出すデータがますます増加していく中で、そのデータをビジネスにどう活用していくかをエンジニアの視点で考えられるすばらしい本だと思います。
今回はこの本の中で特に参考になった点を中心にピックアップしていきます。
🐝 本書のサンプルデータ サポートページ:データサイエンティスト養成読本 [ビッグデータ時代のビジネスを支えるデータ分析力が身につく!]
🐞 データサイエンティストの仕事術 Cross Industry Standard Process for Data Mining(CRISP-DM) データマイニングプロジェクトにおける標準的な6つの手順。
1) Business Understanging
ビジネスの全体像の理解(ヒアリング)と課題設定
2) Data Understanding
データ収集と理解に努めて、仮説構築の下地を作る
3) Data Preparation
数理モデルの作成のために、データマート(データウェアハウス)を構築。
欠損値や外れ値を除去していく。
4) Modeling
仮説に戻ついて、数理モデルを構築する
5) Evaluation
数理モデルの評価。ビジネスリスクの評価
6) Deployment
数理モデルにもとづく、ビジネス施策の実施
必要なスキルセット # ハードスキル
1) Data Understanding 〜 Data Preparation
RDBMS(SQL)、Hadoop(HDFS)、MapReduce、Hiveなど
2) Modeling 〜 Devaluation
統計解析、機械学習の知識、R, Pythonなど
# ソフトスキル
1) Business Understanding 〜 Data Understanding
ビジネスにおける業界、業務の知識。質問力、理解力が必要
2) Deployment
分析結果の伝達力、説得力、プロジェクトの推進力が必要
根本としては好奇心。「問題を核心まで掘り下げて、そこで見付け足疑問を明確で検証可能な一連の仮説に落とし込みたいという欲求 」が必要。
データサイエンスよりも大切なこと 1) 統計的な正しさよりもビジネスの成功
2) 組織の構造や実務の改善効果を重視する
3) 意味のある分析のためには泥臭いクリーニングが必須
4) データは適切な保持が大切
パラメトリックとノンパラメトリック @TJO_datasci
僕自身いくつか文献を見ましたが、まだまだ理解できていません。引き続き勉強して理解できたら、また自分の言葉で書き直したいと思います!
😼 データ分析実践入門 下準備: RStudio 本章では主にRを使います。RStudioについては次の章で説明します。
ロジスティック回帰 Rにデフォルトで入っている、タイタニック号の乗客の生存情報(Titanic)にロジスティック回帰モデルを使う。乗客の各属性から、生存の要因を探す。
## データ整形 z <- data.frame(titanic)< span>titanic.data <- data.frame(< span> Class=rep(z$Class, z$Freq), Sex=rep(z$Sex, z$Freq), Age=rep(z$Age, z$Freq), Survived=rep(z$Survived, z$Freq) ) head(titanic.data) # Class Sex Age Survived # 1 3rd Male Child No # 2 3rd Male Child No # 3 3rd Male Child No # 4 3rd Male Child No # 5 3rd Male Child No # 6 3rd Male Child No ## モデル構築 titanic.logit <- glm(survived~., data="titanic.data," family="binomial)summary(titanic.logit) # Call: # glm(formula = Survived ~ ., family = binomial, data = titanic.data) # # Deviance Residuals: # Min 1Q Median 3Q Max # -2.0812 -0.7149 -0.6656 0.6858 2.1278 # # Coefficients: # Estimate Std. Error z value Pr(>|z|) # (Intercept) 0.6853 0.2730 2.510 0.0121 * # Class2nd -1.0181 0.1960 -5.194 2.05e-07 *** # Class3rd -1.7778 0.1716 -10.362 < 2e-16 *** # ClassCrew -0.8577 0.1573 -5.451 5.00e-08 *** # SexFemale 2.4201 0.1404 17.236 < 2e-16 *** # AgeAdult -1.0615 0.2440 -4.350 1.36e-05 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # (Dispersion parameter for binomial family taken to be 1) # # Null deviance: 2769.5 on 2200 degrees of freedom # Residual deviance: 2210.1 on 2195 degrees of freedom # AIC: 2222.1 # # Number of Fisher Scoring iterations: 4
オッズ比の計算 install.packages('epicalc') library('epicalc') logistic.display(titanic.logit, simplified=T) # OR lower95ci upper95ci Pr(>|Z|) # Class2nd 0.3612825 0.2460447 0.5304933 2.053331e-07 # Class3rd 0.1690159 0.1207510 0.2365727 3.691891e-25 # ClassCrew 0.4241466 0.3115940 0.5773549 5.004592e-08 # SexFemale 11.2465380 8.5408719 14.8093331 1.431830e-66 # AgeAdult 0.3459219 0.2144193 0.5580746 1.360490e-05 #=> 例えば、女性のほうが11.2465380倍生存確率が高いということがわかる
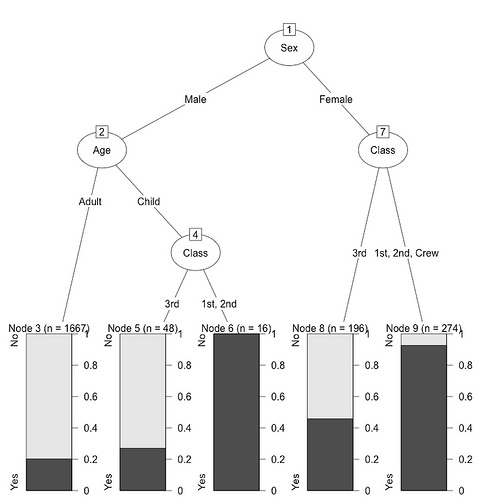
決定木モデル library(rpart) install.packages('partykit') library(partykit) titanic.rp <- rpart(survived~., data="titanic.data)plot(as.party(titanic.rp), tp_args=T)
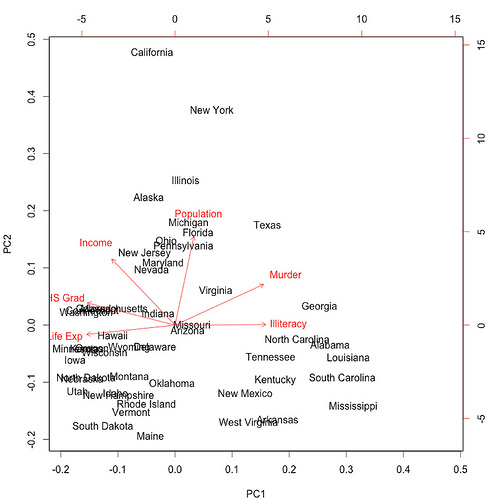
主成分分析 state.pca <- prcomp(state.x77[,1:6], scale="T)biplot(state.pca)
非階層クラスタリング: k-means k-meansの手順。
1) k個のクラスタの中心の初期値を決める
2) 各データをk個クラスタ中心との距離を求め、最も近いクラスタに分類
3) 形成されたクラスタの中心を求める
4) クラスタの中心が変化しない時点まで(2), (3)を繰り返す
サンプルソースはこちら。
# k-meansの実行(クラスタ数を3つに設定) state.km <- kmeans(scale(state.x77[,1:6]),3)< span># 主成分分析の結果にクラスタ情報を付与 state.pca.df <- data.frame(state.pca$x)< span>state.pca.df$name <- rownames(state.pca.df)< span>state.pca.df$cluster <- as.factor(state.km$cluster)< span># 描画 ggplot(state.pca.df, aes(x=PC1, y=PC2, label=name, col=cluster)) + geom_text() + theme_bw(16)
レーダーチャート install.packages('fmsb') library('fmsb') df <- as.data.frame(scale(state.km$centers))< span>dfmax <- apply(df, 2, max) + 1< span>dfmin <- apply(df, 2, min) - 1< span>df <- rbind(dfmax, dfmin, df)< span># 描画 radarchart(df, seg=5, plty=1, pcol=rainbow(3)) legend("topright", legend=1:3, col=rainbow(3), lty=1) # クラスタ1 => 平均寿命、高卒率、収入が多い # クラスタ2 => 殺人件数と非識字率が高い # クラスタ3 => 人口が多い
🐮 RStudioのすすめ 以下オススメリンク。
デスクトップアプリ R用のIDE: RStudio
1) RStudioのコード補完や、関数へのジャンプ、組み込み関数のソース閲覧機能
2) Apacheとの連携によるレポート表示、Emailでのレポート配信
3) Gitによるソースコード管理のサポート機能
knitr
RPubs
RStudio Server
🏈 Pythonによる機械学習 Pythonで使えるデータ分析に有効なライブラリ群についての紹介。
データ分析と機械学習 データ分析において、機械学習は単なる手段のひとつ。
* ある説明変数に対して目的変数がどのくらい影響を与えているかを知ることができる
* 複数の変数から重要な変数を絞り込む事ができる
Python環境の準備 もしMachのPython環境を作る場合は、拙著[Python開発環境構築徹底解説pyenv, mac がオススメです。
Pythonのライブラリ 利用するライブラリのインストール。
# 効率的な数値計算のためのライブラリ pip install numpy # 最適化、補間、積分、統計、画像処理、クラスタリング解析、信号処理、空間的解析などができる pip install scipy # matplotlibのインストール用の設定 ln -s /usr/local/opt/freetype/include/freetype2 /usr/local/include/freetype # グラフ描画ライブラリ pip install matplotlib # ファイルを作成してパラメータを記述 vim ~/.matplotlib/matplotlibrc # ↓ 以下を追加 backend : TkAgg # 機械学習ライブラリ: 単回帰分析〜SVMなどまで対応 # 教師あり学習、教師なし学習、モデル選択のためのクロスバリデーション pip install scikit-learn # データ構造・データ解析のライブラリ:Rのdata.frameなどがある pip install pandas # PythonからR言語を呼び出すためのライブラリ pip install rpy2 # pythonを対話的に実行するためのライブラリ pip install ipython
あやめのデータを知る wget https://dataminingproject.googlecode.com/svn-history/r44/DataMiningApp/datasets/Iris/iris.csv # IRIS.csvのあるフォルダでipythonを起動 ipython # iris.csvを読み込み import pandas as pd iris = pd.read_csv("iris.csv") iris.info() # データ加工 setosa = iris[iris["Species"] == "setosa"] versicolor = iris[iris["Species"] == "versicolor"] virginica = iris[iris["Species"] == "virginica"] # 基本的な統計量 ########################### # 合計 virginica.sum() # Sepal Length 329.4 # Sepal Width 148.7 # Petal Length 277.6 # Petal Width 101.3 # 平均 virginica.mean() # Sepal Length 6.588 # Sepal Width 2.974 # Petal Length 5.552 # Petal Width 2.026 # 中央値 virginica.median() # Sepal Length 6.50 # Sepal Width 3.00 # Petal Length 5.55 # Petal Width 2.00 # 最小値 verginica.min() # Sepal Length 4.9 # Sepal Width 2.2 # Petal Length 4.5 # Petal Width 1.4 # 最大値 virginica.max() # Sepal Length 7.9 # Sepal Width 3.8 # Petal Length 6.9 # Petal Width 2.5 # 相関係数 virginica.corr() # Sepal Length Sepal Width Petal Length Petal Width # Sepal Length 1.000000 0.457228 0.864225 0.281108 # Sepal Width 0.457228 1.000000 0.401045 0.537728 # Petal Length 0.864225 0.401045 1.000000 0.322108 # Petal Width 0.281108 0.537728 0.322108 1.000000 # 分散 virginica.var() # Sepal Length 0.404343 # Sepal Width 0.104004 # Petal Length 0.304588 # Petal Width 0.075433 # 標準偏差 virginica.std() # Sepal Length 0.635880 # Sepal Width 0.322497 # Petal Length 0.551895 # Petal Width 0.274650 # 共分散 virginica.cov() # Sepal Length Sepal Width Petal Length Petal Width # Sepal Length 0.404343 0.093763 0.303290 0.049094 # Sepal Width 0.093763 0.104004 0.071380 0.047629 # Petal Length 0.303290 0.071380 0.304588 0.048824 # Petal Width 0.049094 0.047629 0.048824 0.075433 # ピポッテーブルの作成 import numpy as np pd.pivot_table(iris, rows=["Species"], aggfunc=np.mean) # Petal Length Petal Width Sepal Length Sepal Width # Species # setosa 1.464 0.244 5.006 3.418 # versicolor 4.260 1.326 5.936 2.770 # virginica 5.552 2.026 6.588 2.974
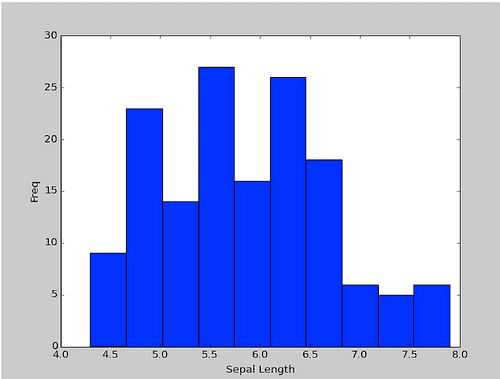
irisでヒストグラムの実行 import matplotlib.pyplot as plt plt.hist(iris["Sepal Length"]) plt.xlabel("Sepal Length") plt.ylabl("Freq") plt.show()
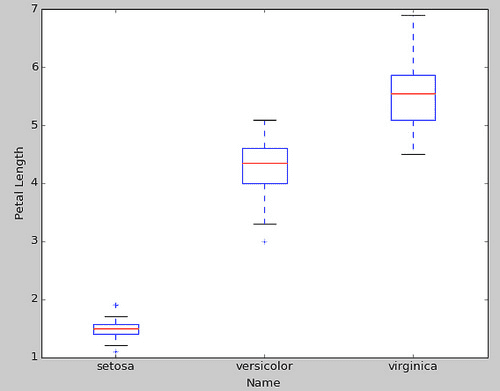
箱ひげ図 data = [setosa["Petal Length"], versiclor["Petal Length"], virginica["Petal Length"]] plt.boxplot(data) plt.xlabel("Species") plt.ylabel("Petal Length") ax = plt.gca() plt.setp(ax, xticklabels=["setosa", "versicolor", "virginica"]) plt.show()
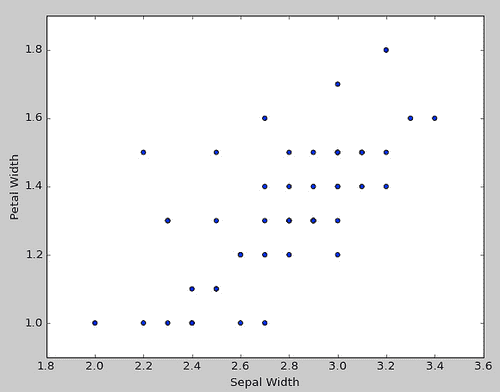
散布図 plt.scatter(versicolor["Sepal Width"], versicolor["Petal Width"]) plt.xlabel("Sepal Width") plt.ylabel("Petal Width") plt.show()
相関係数 # versicolorのSepal WidthとPetal Widthの相関係数 import numpy as np corr = np.corrcoef(versicolor["Sepal Width"], versicolor["Petal Width"]) print(corr[0,1]) #=> 0.663998720024
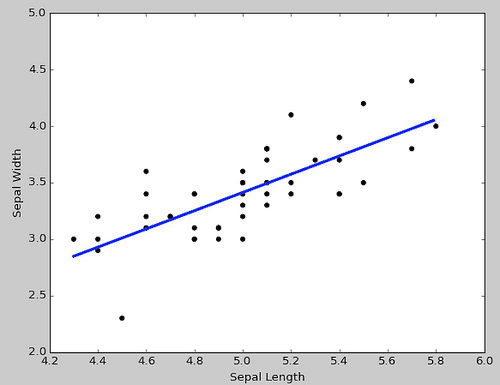
単回帰分析 from sklearn import linear_model LinerRegr = linear_model.LinearRegression() X = setosa[["Sepal Length"]] Y = setosa[["Sepal Width"]] LinerRegr.fit(X, Y) plt.scatter(X, Y, color="black") px = np.arange(X.min(), X.max(), .01)[:,np.newaxis] py = LinerRegr.predict(px) plt.plot(px, py, color="blue", linewidth=3) plt.xlabel("Sepal Length") plt.ylabel("Sepal Width") plt.show()
# 回帰変数 print(LinerRegr.coef_) #=> [[ 0.80723367]] # 切片 print(LinerRegr.inercept_) #=> [-0.62301173]
Rの機能を使って重回帰分析 => rpy2 import rpy2.robjects as robjects robjects.globalenv["SepalLength"] = robjects.FloatVector(setosa["Sepal Length"]) robjects.globalenv["SepalWidth"] = robjects.FloatVector(setosa["Sepal Width"]) robjects.globalenv["PetalLength"] = robjects.FloatVector(setosa["Petal Length"]) robjects.globalenv["PetalWidth"] = robjects.FloatVector(setosa["Petal Width"]) r = robjects.r # Rの重回帰分析 rlm = r.lm("SepalWidth~SepalLength+PetalLength+PetalWidth") print((r.summary(rlm))) # Residuals: # Min 1Q Median 3Q Max # -0.75025 -0.17983 -0.00411 0.15933 0.57704 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) -0.48721 0.56900 -0.856 0.396 # SepalLength 0.79304 0.11162 7.105 6.35e-09 *** # PetalLength -0.09678 0.22875 -0.423 0.674 # PetalWidth 0.31530 0.37186 0.848 0.401 # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.2594 on 46 degrees of freedom # Multiple R-squared: 0.5649, Adjusted R-squared: 0.5366 # F-statistic: 19.91 on 3 and 46 DF, p-value: 2.042e-08
ダミー変数の利用 # 数値データ以外も分析に活用する # Spiciesをダミー変数(品種の0/1のカラム)に変換 import pandas as pd dummies = pd.get_dummies(iris["Species"]) iris = pd.concat([iris, dummies], axis=1)
回帰係数と切片を求める LinearRegr = linear_model.LinearRegression() X = iris[["setosa", "versicolor"]] Y = iris[["Sepal Length"]] LinearRegr.fit(X, Y) # 回帰係数 print(LinearRegr.coef_) #=> [[-1.582 -0.652]] # 切片 print(LinearRegr.intercept_) #=> [ 6.588]
### データマイニングの流れ
1) ゴールを決める
2) 変数の種類・表している事象を知る
3) 1変量の解析を行う。平均値を算出し、ヒストグラム・箱ひげ図を描写
4) 2変量の解析を行う。散布図などのグラフから理解を深める
5) 説明変数を減らして、解釈しやすいモデルに当てはめる
6) 推定された結果を(2)-(4)に振り返ってモデル検証を行う
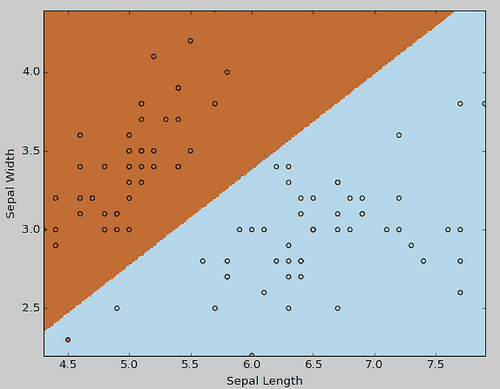
ロジスティック回帰モデル import sklearn use_data = np.logical_or(iris["Species"] == "setosa", iris["Species"] == "virginica") setosa_virginica = iris[use_data] X = setosa_virginica[["Sepal Length", "Sepal Width"]] Y = setosa_virginica[["setosa"]] LogRegr = sklearn.linear_model.LogisticRegression(C=1.0) LogRegr.fit(X,Y) # 偏回帰係数 print(LogRegr.coef_) #=> [[-2.15056433 3.53948104]] # 切片 print(LogRegr.intercept_) #=> [ 0.94024115]
なんか間違っている気がするので、あとで直す予定です。まずはちょっと触れるところから。
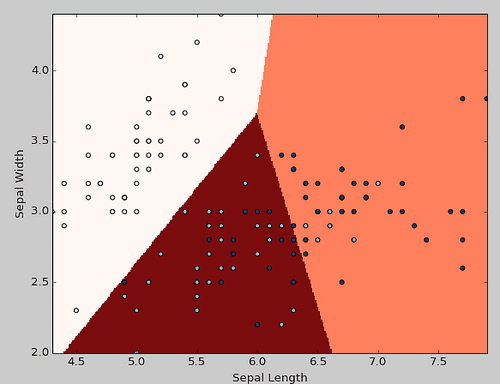
モデル結果をグラフにして確認 xMin = X["Sepal Length"].min() xMax = X["Sepal Length"].max() yMin = X["Sepal Width"].min() yMax = X["Sepal Width"].max() xx,yy = np.meshgrid(np.arange(xMin, xMax, 0.01), np.arange(yMin, yMax, 0.01)) Z = LogRegr.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.figure() plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.xlabel("Sepal Length") plt.ylabel("Sepal Width") plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired) plt.scatter(X["Sepal Length"], X["Sepal Width"], c=np.array(Y), cmap=plt.cm.Paired) plt.show()
🗻 決定木 まずはHomebrewでGraphvizとPythonで使うためのライブラリpydotをインストール。
brew update brew install gts brew install graphviz pip uninstall pyparsing pip install -Iv https://pypi.python.org/packages/source/p/pyparsing/pyparsing-1.5.7.tar.gz#md5=9be0fcdcc595199c646ab317c1d9a709 pip install pydot
続いてIPythonのコンソール。
from sklearn import tree X = iris[["Sepal Length", "Sepal Width", "Petal Length", "Petal Width"]] Y = iris[["Species"]] treeClf = tree.DecisionTreeClassifier(max_depth=2) treeClf.fit(X, Y)
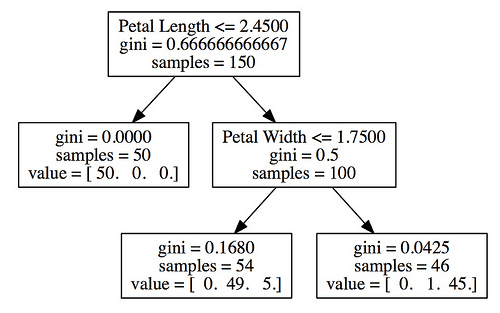
決定木 同じくグラフがなんか違うので、あとで見直す予定。
## 決定木の構築 from sklearn import tree X = iris[["Sepal Length", "Sepal Width", "Petal Length", "Petal Width"]] Y = iris[["Species"]] treeClf = tree.DecisionTreeClassifier(max_depth=2) treeClf.fit(X, Y) ## 決定木の可視化 import StringIO import pydot dot_data = StringIO.StringIO() tree.export_graphviz(treeClf, out_file=dot_data, feature_names=["Sepal Length", "Sepal Width", "Petal Length", "Petal Width"]) graph = pydot.graph_from_dot_data(dot_data.getvalue()) graph.write_pdf("iris_decision_tree.pdf")
k-means法 # k-meansの実行 from sklearn import cluster X = iris[["Sepal Length", "Sepal Width"]] kmeansCls = cluster.KMeans(n_clusters=3) kmeansCls.fit(X) print(kmeansCls.predict(X)) # [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 # 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 # 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 2 2 2 1 2 2 2 2 # 2 2 1 1 2 2 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 2 1 2 2 2 2 1 2 2 2 1 2 2 2 1 2 # 2 1] # k-means法の可視化 import numpy as np import matplotlib.pyplot as plt def category2int(x): category = {"setosa": 0, "versicolor": 1, "virginica": 2} return category[x] f = lambda x: category2int(x) Y = iris["Species"].map(f) xMin = X["Sepal Length"].min() xMax = X["Sepal Length"].max() yMin = X["Sepal Width"].min() yMax = X["Sepal Width"].max() xx,yy = np.meshgrid(np.arange(xMin, xMax, 0.01), np.arange(yMin, yMax, 0.01)) Z = kmeansCls.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.figure() plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.xlabel("Sepal Length") plt.ylabel("Sepal Width") plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Reds) plt.scatter(X["Sepal Length"], X["Sepal Width"], c=np.array(Y), cmap=plt.cm.Blues) plt.show()
👽 データマイニング10のアルゴリズム C4.5 * 決定木を構築する計算アルゴリズム
* 結果のイメージが直感的て理解しやすい
* 分類の精度は高くない
k-meansアルゴリズム クラスタリングでは次のステップを反復して計算。
1) データにクラスタを割り振る(中心と一番近いクラスタを割り振る)
2) クラスタ事の平均値の計算
サポートベクタマシン * 少なめのサンプルで説明変数が多い場合に適した手法
* SVMは特徴量が膨大でも高速に計算できる
* サンプル数が増えると計算時間が急に増加する
アプリケーションオリアルゴリズム * 大量のトランザクションの中から価値あるつながりを見つけるために使われる手法
* 強力な結果が得られる上、実装が比較的容易
EMアルゴリズム Expectation-maximization algorithm(期待値最大化法)。数式展開では計算出来ないような複雑なモデルのパラメータ推定に用いる。以下はその手順。
1) パラメータの初期値を決める
2) Exceptationステップ: 未観測データの期待値を求める
3) Maximizationステップ: 未観測データの期待値を求める
アダブースト * いくつかの学習木を組み合わせることで、強力な予測性能を得る
* 実装が容易で解釈がしやすい
* ディープラーニングが出るまでは最も有力な予測モデルと言われてきた
ナイーブベイズ * クラスを予測するための手法で構築が容易
* テキスト分類やパターン認識で広く利用されている
🎳 Rによるマーケティング分析 R言語で学ぶマーケティング分析 競争ポジショニング戦略
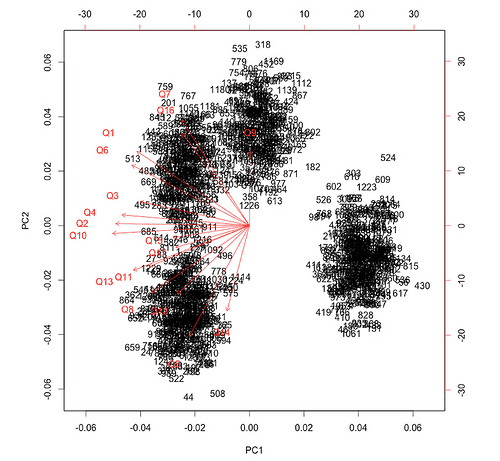
主成分分析の実行 setwd("~/Dropbox/study-R/") # データの読み込み sp.user.data <- read.csv("data sp_user_research_data.csv")< span># 主成分分析 => ユーザー間の類似関係の把握 sp.user.pca <- prcomp(sp.user.data[,-1], scale="T)# バイプロットの表示 biplot(sp.user.pca)
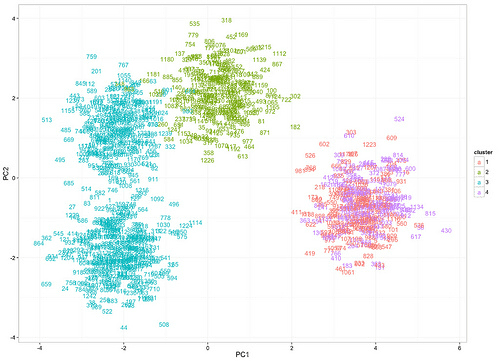
k-meansによるクラスタリングの実行 sp.user.km <- kmeans(sp.user.data[,-1], 4)< span># 主成分分析の結果にクラスタ情報を付与 sp.user.pca.df <- data.frame(sp.user.pca$x)< span>sp.user.pca.df$id <- sp.user.data$id< span>sp.user.pca.df$cluster <- as.factor(sp.user.km$cluster)< span># 描画 install.packages("ggplot2") library("ggplot2") ggplot(sp.user.pca.df, aes(x = PC1, y = PC2, label = id, col = cluster)) + geom_text() + theme_bw(16)
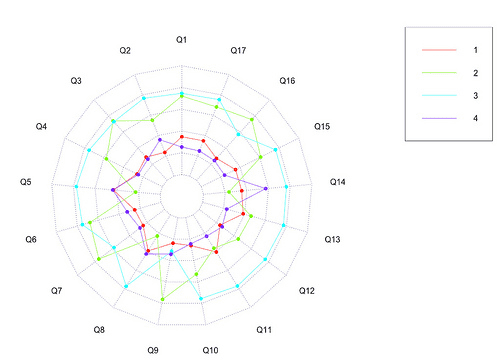
レーダーチャートの作成 install.packages("fmsb") library("fmsb") # レーダーチャート用にデータを整形 df <- data.frame(scale(sp.user.km$centers))< span>dfmax <- apply(df, 2, max) + 1< span>dfmin <- apply(df, 2, min) - 1< span>df <- rbind(dfmax, dfmin, df)< span># レーダーチャートの描画 radarchart(df, seg = 5, plty = 1, pcol = rainbow(4)) legend("topright", legend = 1:4, col = rainbow(4), lty = 1)
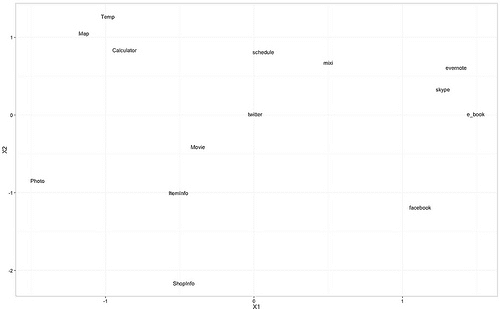
## MDS(Mult-dimentional scaling: 多次元尺度構成法) - 知覚マップ install.packages("MASS") library("MASS") # 先行データの読み込み setwd("~/Dropbox/study-R/data") target.data <- read.csv("target_preference_data.csv", header="T)# 非計算MDSの実行 service.dist <- dist(t(target.data[, -1]))< span>service.map <- isomds(service.dist)< span># 描画用データの整形 service.map.df <- data.frame(scale(service.map$points))< span>service.map.df$service_name <- names(target.data[, -1])< span># 描画 ggplot(service.map.df, aes(x = X1, y = X2, label = service_name)) + geom_text() + theme_bw(16)
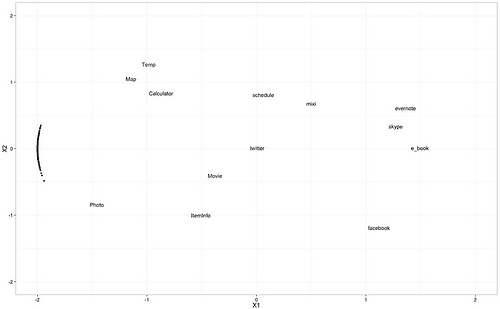
選好ベクトルの推定 # 選好ベクトルの推定 user.preference.data <-< span> do.call(rbind, lapply(1:nrow(target.data), function(i){ preference.data <- data.frame(< span> p=as.numeric(target.data[i, -1]), X1=service.map.df$X1, X2=service.map.df$X2) fit <- lm(p~., data="preference.data) b <- 2 sqrt(fit$coef["x1"]^2+fit$coef["x2"]^2)< span> data.frame(X1=b*fit$coef["X1"], X2=b*fit$coef["X2"], service_name=i) })) # 選好ベクトルの描画 ggplot(service.map.df, aes(x=X1, y=X2, label=service_name)) + geom_text() + theme_bw(16) + xlim(-2,2) + ylim(-2,2) + geom_point(data=user.preference.data, aes(x=X1, y=X2))
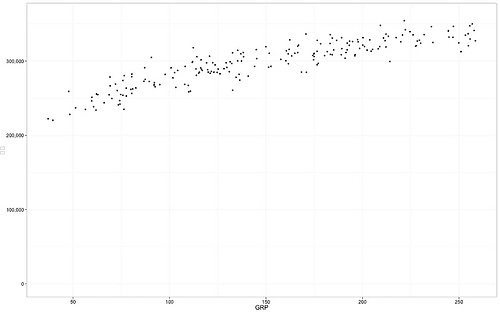
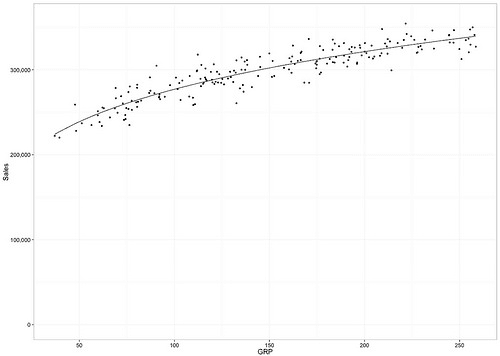
仮想データの読み込みと散布図の描画 # 利用する仮想データの読み込み library(ggplot2) library(scales) # GRPと売上データの読み込み grp.data <- 2013 read.csv("http: image.gihyo.co.jp assets files book 978-4-7741-5896-9 download grp.csv", header="T)# 散布図の描画 ggplot(grp.data, aes(x=grp, y=amount)) + geom_point() + scale_y_continuous(label=comma, limits=c(0,360000)) + ylab("Sales") + xlab("GRP") + theme_bw(16)
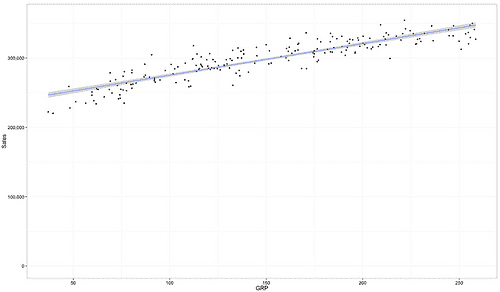
線形型モデルの構築 # 可視化はgeom_smooth関数ですぐにできる ggplot(grp.data, aes(x=grp, y=amount)) + geom_point() + scale_y_continuous(label=comma, limits=c(0, 360000)) + ylab("Sales") + xlab("GRP") + geom_smooth(method = "lm") + theme_bw(16) # モデル構築 fit <- lm(amount~grp, data="grp.data)# モデル概要の表示 summary(fit) # Call: # lm(formula = amount ~ grp, data = grp.data) # # Residuals: # Min 1Q Median 3Q Max # -31521 -8275 321 8701 36962 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 229812.53 2561.73 89.71 <2e-16 ***< span># grp 455.54 15.93 28.60 <2e-16 ***< span># --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 13070 on 198 degrees of freedom # Multiple R-squared: 0.8051, Adjusted R-squared: 0.8042 # F-statistic: 818.1 on 1 and 198 DF, p-value: < 2.2e-16
xx減型モデルの構築 読めなかった。日本語苦手っすw
fit <- lm(log(amount)~log(grp), data="grp.data)# モデル概要 summary(fit) # Call: # lm(formula = log(amount) ~ log(grp), data = grp.data) # # Residuals: # Min 1Q Median 3Q Max # -0.121782 -0.023589 -0.003298 0.025672 0.116504 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 11.546963 0.032379 356.62 <2e-16 ***< span># log(grp) 0.213933 0.006551 32.66 <2e-16 ***< span># --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.04064 on 198 degrees of freedom # Multiple R-squared: 0.8434, Adjusted R-squared: 0.8426 # F-statistic: 1067 on 1 and 198 DF, p-value: < 2.2e-16 # 予測結果を描画 fit.data <- data.frame(grp="grp.data$grp," amount="exp(fit$fitted.values))ggplot(grp.data, aes(x=grp, y=amount)) + geom_point() + geom_line(data=fit.data, aes(x=grp, y=amount)) + scale_y_continuous(label=comma, limits=c(0,360000)) + ylab("Sales") + xlab("GRP") + theme_bw(16)
AとBが同じ場合のA/Bテストのシミュレーション library("plyr") # A/Bの心のコンバージョン率を設定 A1.CVR <- 0.09< span>B1.CVR <- 0.09< span># サンプル数 n <- 10000< span>set.seed(2) # シミュレーション AB1 <- data.frame(pattern="c(rep("A"," n), rep("b", n)), cv="c(rbinom(n," 1, a1.cvr), rbinom(n, b1.cvr)))< span># コンバージョン率の算出 ddply(AB1, .(Pattern), summarize, CVR=mean(CV)) # Pattern CVR # 1 A 0.0942 # 2 B 0.0912 # カイ二乗検定 chisq.test(table(AB1)) # Pearson's Chi-squared test with Yates' continuity correction # # data: table(AB1) # X-squared = 0.5, df = 1, p-value = 0.4795
Bのほうが高い場合のA/Bテストのシミュレーション A2.CVR <- 0.095< span>B2.CVR <- 0.097< span>n <- 10000< span>set.seed(2) # シミュレーション AB2 <- data.frame(pattern="c(rep("A"," n), rep("b", n)), cv="c(rbinom(n," 1, a2.cvr), rbinom(n, b2.cvr)))< span># コンバージョン率の算出 ddply(AB2, .(Pattern), summarize, CVR = mean(CV)) # Pattern CVR # 1 A 0.100 # 2 B 0.097 # カイ二乗検定 chisq.test(table(AB2)) # Pearson's Chi-squared test with Yates' continuity correction # # data: table(AB2) # X-squared = 0.4735, df = 1, p-value = 0.4914
50万件でのシミュレーション A3.CVR <- 0.095< span>B3.CVR <- 0.097< span>n <- 500000< span>set.seed(2) # シミュレーション AB3 <- data.frame(pattern="c(rep("A"," n), rep("b", n)), < span> CV=c(rbinom(n, 1, A3.CVR), rbinom(n, 1, B3.CVR))) # コンバージョン率の算出 ddply(AB3, .(Pattern), summarize, CVR=mean(CV)) # Pattern CVR # 1 A 0.095192 # 2 B 0.097040 # カイ二乗検定の実行 chisq.test(table(AB3)) # Pearson's Chi-squared test with Yates' continuity correction # # data: table(AB3) # X-squared = 9.8061, df = 1, p-value = 0.001739
直交表の作成 install.packages("conjoint") library(conjoint) # 構成要素 experiment <- expand.grid(< span> imgA = c("ImageA1", "ImageA2"), imgB = c("ImageB1", "ImageB2"), txtA = c("TextA1", "TextA2"), txtB = c("TextB1", "TextB2")) # 交流表の作成 design.ort <- cafactorialdesign(data="experiment," type="orthogonal" )< span>design.ort # imgA imgB txtA txtB # 2 ImageA2 ImageB1 TextA1 TextB1 # 3 ImageA1 ImageB2 TextA1 TextB1 # 5 ImageA1 ImageB1 TextA2 TextB1 # 8 ImageA2 ImageB2 TextA2 TextB1 # 9 ImageA1 ImageB1 TextA1 TextB2 # 12 ImageA2 ImageB2 TextA1 TextB2 # 14 ImageA2 ImageB1 TextA2 TextB2 # 15 ImageA1 ImageB2 TextA2 TextB2
ロジスティック回帰モデルの構築 # 仮想のテスト結果データの読み込み(csがないので以下実行していません) web.test.data <- read.csv("web_test_sample.csv")< span># 上位6件だけ表示 head(web.test.data) # ロジスティック回帰モデルの構築 fit <- step(glm(cv~., data="web.test.data[,-1]," family="binomial))# モデル概要 summary(fit)
🍮 Fluentd入門 ログ回収をストリーミングで行ってくれるツール。ツールについての詳しい説明は、創業者の古橋さんのインタビュー記事『グリー技術者が聞いた、fluentdの新機能とTreasure Data古橋氏の野心
ログ解析の従来の課題 1) ログデータの転送に長い時間が必要、帯域の局所的な消費
2) データが解析可能になるまでのタイムラグ
3) ネットワーク障害などによる不安定さ
Fluentdの利点 1) JSON形式で構造化されている
2) 豊富なプラグイン(プラガブル)
3) 導入が容易
4) 耐障害性、バッファ、レジューム機能、可用性
アーキテクチャ 1) input: さまざまなソースからデータを読み取りFluentd用の形式に変換
2) Engine: 入ってきたデータをどのBuffe/Outpuプラグインに渡すかをルーティング
3) Bufferプラグイン: Outputプラグインの前にデータを一時保持する仕組み
4) Outputプラグイン: Bufferプラグインから渡されたデータを書き出す
ログ構造 tag: ログの種類。ルーティングで利用
time: ログが記録されたUNIX時刻
record: JSON形式のログ内容
活用方法 1) ログ収集: ログを集めてS3やHadoopに渡す
2) 統計 + 可視性: ログの統計情報を取得し、グラフ表示系のツールと連携する
3) 検知/通知: しきい値ベースや、データマイニングの異常値検出の通知など
システム構成 forwarder: ログ発生場所に立ち上げてログ回収 => aggregatorに送信
aggregator: 複数workerのためのロードバランシング、複数台構成による冗長化
worker: ログのパースや書き換えなど負荷の高い処理を行う
serializer: workerの処理結果のログを集約して別システムに書き出す
watcher: ログからメトリックスを収集、検知や通知を行う
事例紹介 1) ログの回収: DSPの広告効果のレポーティングのための収集の仕組み
2) nginx ログの可視化: Real Time Bidding(RTB)のツール
🚜 あとがき 中身濃すぎる! 超おもしろかったです^^
🏀 Speical Thanks python - Sudo pip install matplotlib fails to find freetype headers. [OS X Mavericks / 10.9] - Stack Overflow
python - pydot and graphviz error: Couldn’t import dot_parser, loading of dot files will not be possible - Stack Overflow
🖥 VULTRおすすめ
「VULTR VULTR ここ