【書評： 入門統計学検定から多量変数解析・実験計画法まで】基礎固めに最適！　


『統計学がわかる』を読んで基礎の中の基礎が少しずつわかってきたので、ステップアップを目指して『入門統計学 検定から多量変数解析・実験計画法まで』を読み始めました。この本は、推測統計についてわかりやすく、実践的に解説しているテキストです。数式の説明もかなり丁寧に書かれており、統計学の理解を深めるための工夫が随所に凝らされています。

今回はこの本の中で、特に勉強になった部分を中心にメモを書いておきます。


🚕 1章： データ整理(記述的統計学)

記述的統計学とは、実験や調査で集めたデータの特性を明らかにするために平均やばらつき、分布などをもとめて整理する学問。

キーワード

# 量的データ
* 比率データ(比率尺度) : +-*/ : 質量、長さ、年齢、時間、金額
* 間隔データ(間隔尺度) : +-   : 温度(摂氏)、知能指数

# 質的データ
* 順位データ(順序尺度) : >= : 満足度、選好度、硬度
* カテゴリデータ(名義尺度) : 度数カウント : 電話番号、性別、血液型

# 連続変量
=> 重さや長さなどもともと区別されていないデータ

# 離散変量
=> 疾病件数や農家戸数などはじめから区別されているデータ

# 変動係数
=> 標準偏差/平均。英語ではCoefficeient of Variation。ばらつきの相対比較に使える

# 相関係数
=> キュウリは長いほど重い。つまり、「重さ」と「長さ」には正の相関関係がある。相関係数は -1 < r < 1。-1に近付くほど負の相関関係があり、0は相関関係なし、1に近付くほど正の相関関係がある。

例題・章末問題をやってみた

## 例題1-2
parent_height <- c(185.0,169.1,166.2,160.1,166.6,172.1,180.5,169.1,170.9,160.0,168.2,175.5)< span>
child_height  <- c(183.0,167.4,171.0,164.2,173.9,177.0,179.3,172.0,170.6,166.3,170.0,173.0)< span>

sums = 0.0
for (i in 1:12) {
  sums = sums + (parent_height[i] - mean(parent_height))*(child_height[i] - mean(child_height))
}
sums/(sqrt(sum((parent_height - mean(parent_height))^2))*sqrt(sum((child_height - mean(child_height))^2)))
#=> 0.8958307

## 章末
# 問1: データの測定尺度
a) 植物の成長速度 => 間隔データ
b) 植物の病気の有無 => 名義尺度
c) 絶対温度(熱力学温度) => 比率尺度
d) 農家のやりがい、アンケートでの5段階評価 => 順序尺度
e) カレンダーの日付 => 間隔尺度

# 問2
# a) 度数分布表、ヒストグラム
sales <- c(400,15,480,993,600,150,115,50,0,130,3000,500,200,55,2200,1,900,1000,450,400)< span>
area  <- c(60,30,365,190,136,15,37,100,170,70,783,560,50,35,595,200,300,356,155,250) < span>
table(area)
# area
# 15  30  35  37  50  60  70 100 136 155 170 190 200 250 300 356 365 560 595 783 
# 1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1 
hist(area)

Rplot

# b) 平均、分散、標準偏差、変動係数
mean(sales) #=> 581.95
var(sales)  #=> 596000.5
sd(sales)   #=> 772.0107
sd(sales)/mean(sales) #=> 1.326593

mean(area) #=> 222.85
var(area)  #=> 45903.82
sd(area)   #=> 214.2518
sd(area)/mean(area) #=> 0.9614169

# c) 相関係数
cor(sales, area, method="pearson") #=> 0.840888

# こんな方法もある
# cor(sales, area, method="spearman")
# cor(sales, area, method="kendall")

# 問3
data1 <- c(2, 4, 5, 7)< span>
data2 <- c(2, 4, 5, 70)< span>

# 算術平均
mean(data1) #=> 4.5
mean(data2) #=> 20.25

# 幾何平均
source("http://aoki2.si.gunma-u.ac.jp/R/src/univariate.R", encoding="euc-jp")
geomean(data1) #=> 4.090623
geomean(data2) #=> 7.274272

# 比較
mean(data1) > geomean(data1)
mean(data2) > geomean(data2)
#=> 突出して大きな値があっても幾何平均は大きな影響を受けない

Speical Thanks

R – Excel にある一変量統計関数

🏀 2章： 確率分布

確率分布とは、確率変数のそれぞれの値、その発生確率との対応を示したもの。代表的なものとしては、一様分布や正規分布、カイ二乗分布などがある。

キーワード

# 確率分布
## 離散型
* 一様分布: 発生確率が一定の事象の分布(サイコロの目など)
* 二項分布: n回のベルヌーイ試行の成功回数xの分布
(同時に複数個のサイコロを投げる、複数個の製品に含まれる不良品数など)
* ポアソン分布: 稀にしか起こらない事象の発生回数の分布
(1日に受け取る電子メールの件数)

## 連続型
* 正規分布： 試行回数nが大きいときの二項分布の近似分布(身長、体重などの自然現象)
* 標準正規分布： 標準化(平均0, 分散1)した分布。z分布と同義。
* 対数正規分布： 変数xの対数が正規分布となる
* t分布： 母分散の代わりに不偏分散を使った分布
* カイ二乗分布： 自由度(標本数)に応じて決まる分布
* F分布： 2つの母集団から持ってきたカイ二乗、もしくは不偏分散の比による分布

ベルヌーイ試行: AかBのどちらかしか起こらないような事象(コインの表裏など)
不偏分散: 標本から算出する母分散の推定量

例題・章末問題をやってみた

# 例題: 標準化
saibai_a <- c(3063, 2275, 2089, 2855, 2836, 3219, 2817, 2136, 2540, 2263, 2140, 1757, 2499, 2093, 2073)< span>
saibai_b <- c(3157, 2707, 3270, 3181, 3633, 3404, 2219, 2730, 3408, 3203, 2938, 3286, 2920, 3332, 3478)< span>

# 標準化
sai_a_sca <- scale(saibai_a)[,]< span>

#平均(小数点下3桁で四捨五入)
round(mean(sai_a_sca), digits=3) 
#=> 0

# 分散
var(sai_a_sca) 
#=>  1

# 標準偏差
sd(sai_a_sca) 
#=> 1

# 標準化
sai_b_sca <- scale(saibai_b)[,]< span>

# 平均(小数点下3桁で四捨五入)
round(mean(sai_b_sca), digits=3) 
#=> 0

# 分散
var(sai_b_sca)
#=> 1

# 標準偏差
sd(sai_b_sca) 
#=> 1

# 大切なこと => 標準化すると平均0、分散1の標準正規分布になる
# 例題: ポアソン分布
## 3日間でマグニチュード7以上の地震が発生する確率
## 日本でマグニチュード7の地震は過去五年で7回発生している
## 式 => 日数 * ((7.0/5.0) / 365) 
r <- 3 * ((7.0 5.0) 365) #> 0.00115
(exp(1)^r*r)/1 #=> 0.01164002 = 1.164%の確率で地震が発生する

# 章末問題
# 1) 標準化
sales <- c(400,15,480,993,600,150,115,50,0,130,3000,500,200,55,2200,1,900,1000,450,400)< span>
sale_sca <- scale(sales)[,] #> 標準化
round(mean(sale_sca), digits=4) #=> 平均: 0
var(sale_sca) #=> 分散: 1

area  <- c(60,30,365,190,136,15,37,100,170,70,783,560,50,35,595,200,300,356,155,250) < span>
area_sca <- scale(area)[,] #> 標準化
round(mean(area_sca), digits=4) #=> 平均: 0
var(area_sca) #=> 分散: 1

# 2) 歪度・尖度
# 歪度
mean((sales-mean(sales))^3)/(sd(sales)^3) #=> 1.883264
# 尖度
mean((sales-mean(sales))^4)/(sd(sales)^4) #=> 5.876389

# 歪度
mean((area-mean(area))^3)/(sd(area)^3) #=> 1.149286
# 尖度
mean((area-mean(area))^4)/(sd(area)^4) #=> 3.309088

# 3) 標準化・偏差値
(80 - 60)/10 #=>2

10*(80-60)/10 + 50 #=> 70

# 4) パーセンテージ
(1/sqrt(2*3.14))*exp(1)^(-2)

# 5) ポワソン分布
食中毒 <- 20204 (127370000*365) #> 4.345876e-07
食中毒 * 484600 #=> 0.2106012
x <- 0 #> 0回発生

(exp(1)^(-0.21)*0.21^x)/1 #=> 0.8105842
#=> 松江市で食中毒一件も発生しない確率は約81%

🎉 Rの使い方メモ

exp(1) #=> 自然対数の底 2.718...
round(num, digits=n) #=> 四捨五入

😀 第3章不偏推定量と標本分布(推測統計学)

推測統計学とは、実験や調査で測定したデータを使ってその背景にある母集団の特徴を推定する学問。平均やバラツキに関する区間推定や差の検定などがある。

キーワード

母集団 => 英語ではpopulationとuniverseがある
population => 標本の背景にあって対象となる要素の集合体(一般的な母集団)
universe => 要素を含む対象自体の集合、関連する情報が付随している

標本のばらつき(標本分散、標本標準偏差) =< 母集団のばらつき(母分散、母標準偏差)
不偏推定量　　<= 母集団の統計量を推定した値 不偏分散　　　<="母集団の分散の推定量" 不偏標準偏差　<="母集団の標準偏差の推定量" 標本誤差分散　<="複数標本間の誤差の分散" < pre>


例題・章末問題
# 例題: 不偏分散誤差
## 栽培法A
### 標本標準偏差を使う場合
標本標準偏差 <- 413.5< span>
標本数 <- 15< span>
標本標準偏差/sqrt(標本数 -1) #=> 110.5
### 不偏標準偏差を使う場合
不偏標準偏差 <- 428.1< span>
不偏標準偏差/sqrt(標本数) #=> 110.5

## 栽培法B
### 標本標準偏差を使う場合
標本標準偏差 <- 353.0< span>
標本数 <- 15< span>
標本標準偏差/sqrt(標本数 -1) #=> 94.3
### 不偏標準偏差を使う場合
不偏標準偏差 <- 365.4< span>
不偏標準偏差/sqrt(標本数) #=> 94.3

# 章末問題
# 問1)
# 母集団 : 新入生1万人(試験結果)
# 標本 : 無作為に抽出した500人
# ユニバース : 新入生1万人(対象の人間そのもの)
# 標本数 : 1(標本サイズは500)

# 問2)
# 標本分散 =< 母分散となる

# 問3) 標準偏差と標準誤差の違い
# 標準偏差 : 個々のデータからなる集団のバラ付き具合を示す統計量
# 標準誤差 : 標本平均のバラつき具合を示す。不偏統計量の精度を示す指標。

# 問4) 統計量の自由度
# 標本から相関計測を推定する場合、統計量の自由度は「標本サイズ - 2」となる
# (相関係数の場合は変数が2つになるので)


 🎃 4章 : 信頼区間の推定
真の平均や分散が、どのような範囲にあるかを推定し、それを確率的に示すこと。


例題・章末問題
# 例題: 正規分布による95%信頼区間
標本数 <- 16< span>
平均   <- 10.0< span>
母分散 <- 36.0< span>

平均 - 1.96*sqrt(母分散/標本数) #=> 7.06
平均 + 1.96*sqrt(母分散/標本数) #=> 12.94

# 例題: 正規分布による90%信頼区間
月平均の減少値 <-165.0< span>
標本サイズ     <- 66< span>
標本標準偏差   <- 680.6< span>

月平均の減少値 - 1.65*標本標準偏差/sqrt(標本サイズ) #=> 26.76949
月平均の減少値 + 1.65*標本標準偏差/sqrt(標本サイズ) #=> 303.2305

# 例題: t分布による95%信頼区間
標本数 <- 5< span>
平均乳量 <- 22.1< span>
標本芳醇偏差 <- 6.5< span>

22.1 - 2.776*6.5/sqrt(標本数 -1) #=> 17.44106
22.1 + 2.776*6.5/sqrt(標本数 -1) #=> 26.75894

# 例題: 母比率の信頼区間の推定
0.7 - 1.96*sqrt(0.7*(1.0-0.7)/50) #=> 0.5729775
0.7 + 1.96*sqrt(0.7*(1.0-0.7)/50) #=> 0.8270225
#=> 下限の信頼限界が50%を超えているので、当確を出しても良い

# 例題: 標本サイズの決め方

1.96 * sqrt(0.5*0.5/n) = 0.1
# 上の式を満たすnは次の式から求められる
n <- ((1.96 * sqrt(0.5*0.5)) 0.1)^2 #> 96.04

## 章末
# 問1) 標準偏差を使った95%信頼区間
標本サイズ <- 100< span>
標本平均   <- 2.0< span>
標本分散   <- 1.0< span>

標本平均 - 1.96 * sqrt(標本分散/標本サイズ) #=> 1.804
標本平均 + 1.96 * sqrt(標本分散/標本サイズ) #=> 2.196

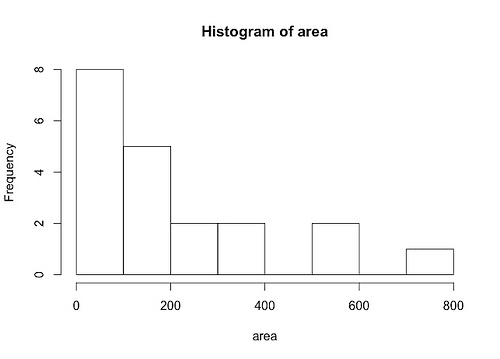
# 問2) t分布を使った95%信頼区間
sales <- c(400,15,480,993,600,150,115,50,0,130,3000,500,200,55,2200,1,900,1000,450,400)< span>
標本サイズ <- length(sales)< span>
標本平均   <- mean(sales)< span>
標本分散   <- var(sales)< span>

標本平均 - 2.093 * sqrt(標本分散/(標本サイズ-1)) #=> 211.2559
標本平均 + 2.093 * sqrt(標本分散/(標本サイズ-1)) #=> 952.6441

# 問3) AgrestiとCoullの式を使った母比率の信頼区間
標本サイズ <- 20< span>
比率 <- 16 20< span>

p <- (16+2) (標本サイズ+4)< span>
p - 1.96*sqrt(p*(1-p)/(標本サイズ+4)) #=> 0.5767588
p + 1.96*sqrt(p*(1-p)/(標本サイズ+4)) #=> 0.9232412

# 問4) 標本サイズの決め方
1.96*sqrt((0.5*0.5)/n) = 0.01
n <- ((1.96 0.01)*sqrt(0.5*0.5))^2 #> 9604
n*5 #=> 48020


🐞 5章： カイ二乗分布とF分布
カイ二乗分布は標準変化量zを2情和したカイ二乗値が従う確率分布で、母分散の信頼区間の推定やクロス集計表の検定に用いる。F分布は独立した2つのカイ二乗値の比であるF値が従う確率分布で、等分散性の検定や分散分析などに用いる。


例題・章末問題をやってみた
# 例題 : 信頼区間95%の母分散
tento <- c(5, 8, 10, 11, 15)< span>
size <- length(tento)< span>
var <- var(tento)< span>

((size - 1)*var)/11.143 #=> 4.917886
((size - 1)*var)/0.484  #=> 113.2231

# 章末問題
# 問1) カイ二乗値とは？
#=> 標準変化量zを2乗和(すべての標準変化量を2乗して足し合わせた値)した値

# 問2) 母平均が未知の場合のカイ二乗値
#=> 未知の場合には、不偏統計量と同様に自由度は減少する
#=> 具体的には、自由度 <- n(標本サイズ) - 1< span>

# 問3) 母標準偏差に対する90%信頼区間
size <- 10< span>
不偏標準偏差 <- 0.05< span>
不偏分散 <- 25< span>

sqrt(((size-1)*不偏分散)/16.919) #=> 3.646733
sqrt(((size-1)*不偏分散)/3.325)  #=> 8.226127

# 問4) t値とF値の関係 
#=> 自由度がvのt値の2乗と、分母の自由度がvで分子の自由度が1のF値は等しい
#=> 2つの平均値の差はt検定(両側検定)でも、F検定を基礎とした2群の分散分析でも同じ結論となる


🐯 6章 : 検定の基礎
仮説検定とは、実験結果の「起きやすさ」から「めったに起きないことが起きた」とかんがえられる場合は、その仮説を間違いであると判断する手法。


検定の手順
1) 仮説の設定
2) 検定統計量の計算
3) 確率の計算
4) 仮説の判断




キーワード
第一種の誤り(Type I error) : 帰無仮説が正しいにもかかわらず棄却してしまうこと
第二種の誤り(Type II error) : 帰無仮説が間違っているにもかかわらず許容すること
危険率 : 第一種の誤りを犯す確率
検定力 : 帰無仮説が間違っている時に正しく棄却できる確率(第二種の誤りを防ぐ)




例題をやってみた
# 例題 : テントウが新種か否かの検定
ave <- 11< span>
既存種の平均 <- 5< span>
誤差 <- 2< span>

#=> 帰無仮説 : 新種ではない
#=> 対立仮説 : 新種である
既存種の平均 - 1.96*誤差 #=> 1.08mm
既存種の平均 + 1.96*誤差 #=> 8.92mm
#=> よって11mmは8.92mmより大きいので帰無仮説が棄却
#=> 新種であると考えたほうが妥当

🖥 VULTRおすすめ

「VULTR」はVPSサーバのサービスです。日本にリージョンがあり、最安は512MBで2.5ドル/月($0.004/時間)で借りることができます。4GBメモリでも月20ドルです。 最近はVULTRのヘビーユーザーになので、「ここ」から会員登録してもらえるとサービス開発が捗ります！

📚 おすすめの書籍