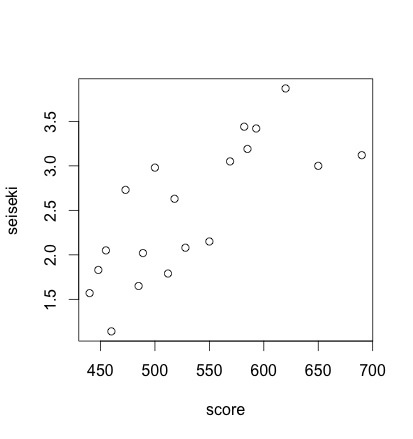
score <- c(440, 448, 455, 460, 473, 485, 489, 500, 512, 518, 528, 550, 582, 569, 585, 593, 620, 650, 690)< span>
seiseki <- c(1.57, 1.83, 2.05, 1.14, 2.73, 1.65, 2.02, 2.98, 1.79, 2.63, 2.08, 2.15, 3.44, 3.05, 3.19, 3.42, 3.87, 3.00, 3.12)< span>
hyotei <- c(5.7, 6.8, 6.2, 5.5, 6.0, 7.3, 7.6, 5.6, 6.5, 7.8, 7.5, 8.2, 7.2, 8.8)< span>
dat <- data.frame(score, seiseki, hyotei)< span>
# 1) 重回帰モデルの式
#=> 学業成績 = a*評定平均 + b*入試点数 + c
# 2) 重回帰モデルの算出
result <- glm(seiseki~score+hyotei, data="dat," family="gaussian)
summary(result)
# Call:
# glm(formula = seiseki ~ score + hyotei, family = gaussian, data = dat)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -0.69843 -0.36003 -0.05394 0.31981 0.77518
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -2.094111 1.003309 -2.087 0.05322 .
# score 0.006935 0.002337 2.968 0.00907 **
# hyotei 0.128121 0.182587 0.702 0.49295
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# (Dispersion parameter for gaussian family taken to be 0.265645)
#
# Null deviance: 10.4396 on 18 degrees of freedom
# Residual deviance: 4.2503 on 16 degrees of freedom
# AIC: 33.468
#
# Number of Fisher Scoring iterations: 2
#=> a = 0.006935, b = 0.128121, c = -2.094111
# 3) 重相関係数 => http://aoki2.si.gunma-u.ac.jp/R/multiple-cor.html
source("http://aoki2.si.gunma-u.ac.jp/R/src/multiple_cor.R", encoding="euc-jp")
multiple.cor(dat)
# score seiseki hyotei
# 0.8141785 0.7699771 0.7020678
#=> 0.7699771
|