今回は、『AOJ 10029 - ソートアルゴリズム(マージソート)
🏀 概要
未整列のデータ群を半分に分ける操作を繰り返す
データ群が分割できなくなったところで今度は分割データのマージを繰り返す
マージはデータが整列するよう行う
🐡 Rubyコード class Array def merge_sort return self if length <= 1 a, b = half.map(&:merge_sort ) merge(a, b) end def half n = (length/2.0 ).floor return self [0 ...n], self [n..(length-1 )] end private def merge (a, b) result = [] while a.size > 0 || b.size > 0 result << if a.empty? then b.shift elsif b.empty? then a.shift elsif a.first < b.first then a.shift else b.shift end end result end end _n = gets.to_i puts gets.split(' ' ).map(&:to_i ).merge_sort.join(' ' )
😼 2つのサンプルを使って比較 2つのランダムな配列を使ってテストをします。2つのサンプルは次のように作成します。
* 0-100000の数字を100,000個、ランダムに並べる場合
* 0-100の数字を100,000個、ランダムに並べる場合
比較結果は次のとおり。
puts Benchmark::CAPTION puts 'quick_sort: ' + Benchmark.measure { sample.quick_sort }.to_s puts 'marge_sort: ' + Benchmark.measure { sample.merge_sort }.to_s puts 'ruby_sort: ' + Benchmark.measure { sample.sort }.to_s puts Benchmark::CAPTION puts 'quick_sort: ' + Benchmark.measure { sample.quick_sort }.to_s puts 'marge_sort: ' + Benchmark.measure { sample.merge_sort }.to_s puts 'ruby_sort: ' + Benchmark.measure { sample.sort }.to_s
マージソートはどちらも安定していますが、クイックソートは入力の配列に寄っては計算量がかなり増加しています。これはクイックソートが入力の配列によっては、1:N-1のソートを繰り返すためとのこと。
クイックソート - Wikipedia
マージソート - Wikipedia
ちなみに、RubyのCでのソートアルゴリズムもクイックソートだそうですが、このあたりもきちっと考慮されているようです。こういった部分も普段からRuby(言語開発者の方々)の恩恵に預かっています。
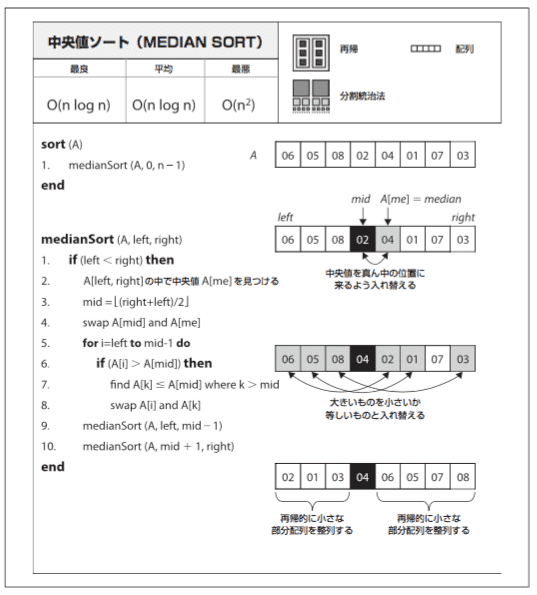
特徴
中央値を効率的に選択する必要がある
最悪時にO(nの2乗)、平均でO(n log n)となる
n個の要素がすべて整列している場合は、全体性能が落ちてしまう
🎉 GitHubリポジトリ Ruby/PythonでのAOJの回答は下のリポジトリに保存しています。
morizyun/aoj-ruby-python - GitHub
🤔 参考リンク
🍮 (参考) 中央値ソート (Median Sort)
クイックソートとの違いは中央値を探し出す点。中央値を効率敵に探し出せれば、
🖥 VULTRおすすめ
「VULTR VULTR ここ